1. Алгебра
  2. сделать, оочень метод

сделать, оочень метод інтервалів)​ ">

Dima2002dg Dima2002dg    2   28.07.2020 14:04    0

Ответы
илья1899 илья1899  15.10.2020 15:31

1) x\in(-\infty; 5]\cup[-4; 0]\cup[4; +\infty)

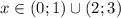
2) x\in(0;1)\cup(2; 3)

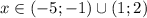
3) x\in(-5;-1)\cup(1; 2)

4) x\in(-\infty;-7]\cup(-5; 1]\cup(5; +\infty)

Объяснение:

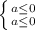
1. Возможны 2 случая когда произведение a*b может быть \left \{ {{a\geq0 } \atop {b\geq0}} \right.или \left \{ {{a\leq0 } \atop {a\leq0}} \right

\left \{ {{x^{2}+5x\geq 0} \atop {x^{2}-16\geq 0}} \right. \\\left \{ {{x^{2}+5x\leq 0} \atop {x^{2}-16\leq 0}} \right.

2. Решить неравенства относительно x:

\left \{ {{x\in(-\infty;-5]\cup[0; +\infty)} \atop {x\in(-\infty;-4]\cup[4; +\infty)}} \right. \\\left \{ {{x\in[-5;0]} \atop {x\in[-4;4]}} \right.

3. Найти пересечения

x\in(-\infty; -5]\cup(4; +\infty)\\x\in[-4;0]

4. Найти объединение

x\in(-\infty; 5]\cup[-4; 0]\cup[4; +\infty)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
пецааааа1 пецааааа1  06.11.2019 13:31
Выпишите шесть первых членов арифметической прогрессии (an),в которой : а) а1 = 15, d = -4б) a2 = -32, d = 8объясните как делать​...
SlowMoe SlowMoe  06.11.2019 13:29
Найти область значения функции...
yuliyakoshka0 yuliyakoshka0  06.11.2019 13:23
кто на какой нибудь вопрос может ответить ❤️...
НастяПи НастяПи  06.11.2019 13:22
Построить графики y=4x, y= - 3x, y=1,5x, y= - 0,4x №2 точка а(2; 9) принадлежит графику прямой пропорциональности. принадлежат ли точки в(1; 4,5), с(-10; 45) и d(-9; 2) !...
Lenka5891 Lenka5891  06.11.2019 13:21
Флорист должен продать 100 цветов за 100 $. если каждый фикус стоит 10 $, каждый хризантемы стоит 3$ и каждый фиалка стоит 0,5 $, то сколько всего хризантем продаст флорист? выберите...
97shadesofblue 97shadesofblue  21.07.2019 01:40
Представьте в виде куба двучлена выражение а3+3а2+3а+1...
BlackJack11RUS BlackJack11RUS  21.07.2019 01:40
Решить уравнения 1) 4x^2 - 4x + 1 = 0 2) x^2 - 16x - 17 = 0 3) 0,3x^2 + 5x = 2 4) x^2 - 4x + 5 = 0 хотя бы одно,...
yuraaverchenko yuraaverchenko  21.07.2019 01:50
Представьте в виде многочлена x(x-1)(x-2)-x^2(x-3)...
Ксения61831378 Ксения61831378  17.04.2020 02:37
По графику производной функции y = f (x) определите, в какой точке отрезка [-1; 2] функция y = f(x) принимает наименьшее значение....
gorlatenkoviktoria gorlatenkoviktoria  17.04.2020 02:37
Выберите верный вариант ответа. При каком целом значении k верно равенство (-3)k=1/729 ? 1. ни при каком 2. -6 3. 6 4. другой ответ...

Популярные вопросы