Самостоятельная работа, 8 класс. Уравнения, сводящиеся к квадратным.
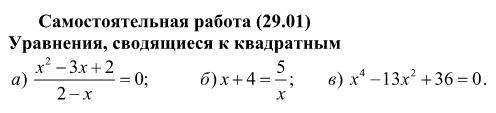
Другие вопросы по теме Алгебра
Популярные вопросы
- Космический корабль,летящий со второй космической скоростью(скорость,необходимая...
2 - Удивительная теплота плавления ртути 12 кдж/кг что это значит...
3 - До какой температуры надо нагреть газ при постоянном давлении,...
2 - How is english used in international commucation? желательно дать...
1 - Составьте 5пословиц или поговорок чтоб в одной пословице были слова...
3 - Сообщение об особенностях жизни сербов...
1 - Урозчині масою 280 г міститься 56 г солі. яка концентрація цього...
3 - Рассказ о воспоминаниях о крестовом походе от лица участника....
2 - На индивидуалке. училка ушла на 5 минут. сколько будет 802мин.÷...
2 - Тело массой 5 кг свободно падает с высоты 80 м. какую скорость...
1
Объяснение:
ну, в примере под а), у нас в числителе квадратное уравнение
и для начала, ОДЗ. думаю знаете, что на ноль делить нельзя, а если корень получится равным 2, то в знаменателе будет 0. поэтому x не может быть равным 2
дискриминант = 9-8=1 (b^2-4ac) (3^2-4*1*2)
х первое = (3-1)/2=1
x второе = (3+1)/2=2 - фантомный корень, такой нам не подойдет.
значит ответ:1
под б перенесем все в одну сторону
x+4-(5/x)=0 и приведем к общему знаменателю
(x^2+4x-5)/x=0 тут ОДЗ проще, просто x не равен нулю.
дискриминант 16+4*5=36=6^2
х первое = (-4-6)/2=-5
x второе (-4+6)/2=1
все корни подходят, ответ -5 и 1
под в это БИквадратное уравнение, нужно заменить x^2 на t (или любую другую переменную)
t^2-13t+36. дискриминант 169-4(36)=25=5^2
t первое = (13+5)/2 = 9
t второе = (13-5)/2=4
теперь возвращаемся к x^2. раз t=x^2=4, значит x=±2
раз t=x^2=9, значит x=±3
ответ: -2, +2, -3, +3.