с заданием по алгебре 8 класс
1)Выполните действие:
х+4/2х-6 - х+1/х-3
2)У выражение:
2ху-у^2/3 * 9х/у^5.
Надеюсь понятно...Очень нужно

Ответы

maria22890 18.08.2020 19:35

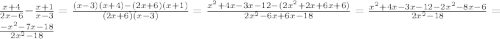1) $\frac{x+4}{2x-6} - \frac{x+1}{x-3} = \frac{(x-3)(x+4)-(2x+6)(x+1)}{(2x+6)(x-3)} = \frac{x^2+4x-3x-12-(2x^2+2x+6x+6)}{2x^2-6x+6x-18} = \frac{x^2+4x-3x-12-2x^2-8x-6}{2x^2-18} = \frac{-x^2-7x-18}{2x^2-18}$ 2)

$\frac{2xy-y^2}{3}* \frac{9x}{y^5} = y(2x-y)*\frac{3x}{y^5} = (2x-y)* \frac{3x}{y^4} = \frac{6x^2-3xy}{y^4}$

ПОКАЗАТЬ ОТВЕТЫ

supermosyagina 09.01.2024 15:29

1) Для выполнения этого действия нам нужно сначала привести дроби к общему знаменателю. Общим знаменателем для обеих дробей будет (2х - 6)(х - 3).

Для первой дроби (х + 4)/(2х - 6) умножим числитель и знаменатель на (х - 3), чтобы получить общий знаменатель:
(х + 4)(х - 3)/[(2х - 6)(х - 3)].

Аналогично для второй дроби (х + 1)/(х - 3) умножим числитель и знаменатель на (2х - 6):
(х + 1)(2х - 6)/[(х - 3)(2х - 6)].

Теперь мы можем объединить дроби:
[(х + 4)(х - 3) - (х + 1)(2х - 6)]/[(2х - 6)(х - 3)].

Раскроем скобки:
[х^2 - 3х + 4х - 12 - (2х^2 + 2х - 6х - 6)]/[(2х - 6)(х - 3)].

Упростим:
[х^2 - 3х + 4х - 12 - 2х^2 - 4х + 6х + 6]/[(2х - 6)(х - 3)].

Теперь сложим и упростим подобные члены:
(-х^2 + 3х - 6)/[(2х - 6)(х - 3)].

Это будет окончательным ответом.

2) Для выполнения этого умножения мы будем использовать правило умножения дробей. Умножение двух дробей выполняется путем умножения числителей и знаменателей.

Мы имеем следующее выражение: (2ху - у^2/3) * (9х/у^5).

Умножим числитель первой дроби (2ху - у^2) на числитель второй дроби (9х), а затем знаменатель первой дроби (3) на знаменатель второй дроби (у^5):

(2ху - у^2) * 9х / (3 * у^5).

Для умножения числителей, перемножим каждый терм первой дроби на вторую дробь:
2ху * 9х - у^2 * 9х / (3 * у^5).

Упростим:
18х^2у - 9ху^2 / (3 * у^5).

Итак, окончательный ответ будет:
18х^2у - 9ху^2 / (3 * у^5).

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра