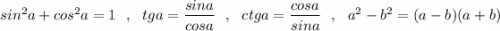с с заданием по алгебре
3 задание,докажите тождества

Другие вопросы по теме Алгебра
Популярные вопросы
- Найди периметр треугольника abc со сторонами ab-3 см bc- 6 см ca- 7 см....
3 - Рассчитайте длину нихромовой проволоки площадью поперечного сечения 0.05 мм^2,...
2 - Построить график функции y=2-x^2 на каком промежутке функция убывает?...
3 - Кшарику заряженного электроскопа поднесите, не касаясь его, заряженный металлический...
2 - Бегун пробежал 50 м за 5 секунд.найдите среднюю скорость бегуна на дистанций....
3 - Укажите на многозначное слово: 1) газета 2)тетрадь 3) стол 4) книга 5) операция...
3 - 21+9+6=20 нужно переставить одну спичку в левой части, правую не трогать...
1 - Составить общий вопрос для: every evening peter walks his dog. he studies english...
1 - Выписать основные, амфотерные и кислотные оксиды: na2o, n2o3, naoh, hno3, cuo2,...
1 - Вычислите значение выражения 9^3/2+27^2/3+81в корне...
3
Объяснение:
3.
Использовали формулы: