С РЕШЕНИЕМ Уравнение x4+ax2+b=0 имеет ровно три корня. Сколько корней имеет уравнение x4+bx2+a=0?

2 корня

Объяснение:

x⁴+ax²+b=0

Данное уравнение является биквадратным и должно иметь 4 корня. По условию, оно имеет три корня, т.е. три действительных корня.  При b=0 это возможно.

Покажем это:

Замена: x²=y

y²+ay+b=0

При b=0  y²+ay=0

                y(y+a)=0

                y=0   или  y+a=0

                                  y=-a

Обратная замена: y=x²

                x²=0  или   x²= -a

                x₁=0           x₂=√-a      x₃=-√-a

Итак, уравнение x⁴+ax²+b=0 имеет три корня

При b=0 уравнение x⁴+bx²+a=0  при b=0 преобразуется в уравнение

x⁴+a=0

x⁴= -a

Получаем, что это уравнение имеет два корня

Легко заметить, что оба уравнения имеют корни x=±1

Уравнение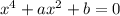

имеет корни:  x=±1

значит

    ⇒    

Уравнение принимает вид:

Третий корень только

при

Тогда

Уравнение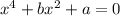

при    и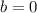  

принимает вид:

и имеет два корня x=±1