с алгеброй Вычисли площадь фигуры, ограниченной линиями:
y=−√6−x,x=−7,y=0.
Другие вопросы по теме Алгебра
Популярные вопросы
- 1.Прочитайте текст. Определите, какие из приведённых утверждений 1—7 соответствуют...
3 - Решите тест как можно быстрей!! Прочитайте текст и выполните задания 1 -...
3 - Сор по матем за 4четверть 5класс...
3 - У выражение: 3(а2 – х2) – (а – х)(а + х)....
1 - Na2SiO3 + HCl → допишите уравнение (разберите его в ионном виде)СuSO4 +...
1 - У квадрата отрезали 4 угла. сколько углов стола?...
3 - Про яку битву йдеться в уривку історичного джерела: «Ольгерд… пішов у похід...
3 - Эссе на тему какой бы я хотел принять закон ...
2 - Какими металлами образуется Me(OH)2...
3 - Oad Proому світі19. Мешканці Долини мумі-тролів мають свій они муМl-тролів...
3
По функции видно, что верхним пределом будет x=6.
ответ: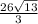
Объяснение:
ответ: S≈31, 2481 кв. ед.