Розвязати нерівність a|x|< і x(6-x квадрате)> 0

a|x|<0

для будь-якого х: |x|>=0;

тому якщо a>0 нерівність   a|x|<0 розвязку немає, зліва додатна величина

якщо а=0, то нерівність має вигляд 0х<0, яка розвязків немає

якщо a<0, то a|x|<0 рівносильна нерівності |x|>=0 і її розвязком буде будь-яке дійсне число

обєднуючи якщо a>=0 то розвязку немає,

якщо a<0, то розвязкок - будь-яке дійсне число, (x є R, x є ))

x(6-x квадрате)>0

чи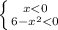

розвязуємо першу систему

розвязуємо другу систему

обєднуючи х є [tex] (-\infty; -\sqrt{6}) \cup (0;6)}

a|x|<0;

|x|≥0 - по определению модуля;

Отсюда параметр:

1) Для а<0:

-a*|x|<0;

x∈R, кроме 0, т.к. неравенство строгое;

2) Для а=0:

0*|x|<0;
Значение данного выражения не может быть меньше 0, то есть решений нет;

3) Для а>0:

а*|x|<0;

Произведение двух положительных чисел не может быть отрицательным, то есть решений нет.

x∈(-∞;0)U(0;+∞) при a<0;

x∈Ф(пустое мн-во) при a≥0.

2. x(6-x²)>0;

x(x²-6)<0;

x(x-√6)(x+√6)<0;

x=0; x=√6; x=-√6;

ответ: x∈(-∞;-√6)U(0;√6).