1. Алгебра
  2. Розв яжiть рiвняння / х+ +2y-3

Розв'яжiть рiвняння / х+ +2y-3 +x²-xy+4y²=0.

муслима18 муслима18    3   31.05.2023 02:33    0

Ответы
Vftfg Vftfg  31.05.2023 06:00

Решить уравнение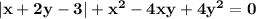     \bf |x+2y-3|+x^2-4xy+4y^2=0  .  

\bf \star \ \ x^2-4xy+4y^2=x^2-2\cdot x\cdot 2y+(2y)^2=(x-2y)^2\ \ \star  

Запишем уравнение в виде

\underbrace{\bf |x+2y-3|}_{\geq 0}+\underbrace{\bf (x-2y)^2}_{\geq 0}=0  

Получили сумму двух неотрицательных слагаемых, которая равна 0 . Это может быть лишь в случае, когда оба слагаемых одновременно равны 0 .

\left\{\begin{array}{l}\bf |x+2y-3|=0\\\bf (x-2y)^2=0\end{array}\right\ \ \left\{\begin{array}{l}\bf x+2y-3=0\\\bf x-2y=0\end{array}\right\ \ \left\{\begin{array}{l}\bf 2y+2y-3=0\\\bf x=2y\end{array}\rightleft\{\begin{array}{l}\bf 4y=3\\\bf x=2y\end{array}\right\ \ \left\{\begin{array}{l}\bf y=0,75\\\bf x=1,5\end{array}\right  

ответ:   х=1,5  , y=0,75  .


Розв'яжiть рiвняння / х+ +2y-3 +x²-xy+4y²=0.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
vikasibarik vikasibarik  20.05.2020 09:31
До параболи y=x^2+ax-9 проведено дотичну під кутом 45⁰. За якого значення параметра а абциса точки дотику дорівнює -5?...
Алена11д1 Алена11д1  20.05.2020 09:32
с алгеброй(логарифмы) 10 класс. это 4 разных выражения. в профиле такое же задание за...
дюха4004 дюха4004  03.03.2020 16:37
Постройте график а) y=-4(x-2) ²-1 б) y=0, 5(x+4) ²+1...
znania53 znania53  03.03.2020 16:37
1.Найди корень уравнения 16x+11=0 . a) −1,81 б) Бесконечно много решений в) x∈∅ г) Нет верного ответа 2.При каких значениях a сумма дробей 3a+2a и 2a−12a равна 1? (Не выделяй...
Motiby19 Motiby19  03.03.2020 16:39
Расстояние между двумя пристанями равно 72,8 км. Из них одновременно навстречу друг другу вышли две лодки, скорости которых в стоячей воде равны. Через 1,3 ч. лодки встретились....
Knzke3 Knzke3  03.03.2020 16:39
Представьте в виде многочлена а) -4a^3*(a^2-3a+2) б) (1-x)(2y+x) в) (5c-4) всё это во второй степени...
Танюшка364 Танюшка364  03.03.2020 16:39
Help! Без понсюятия как решить, тупой как дуб!...
LOLLIPOPS45 LOLLIPOPS45  03.03.2020 16:40
Вкладчик положил в банк 3000 грн на два разных депозитных счета, причем на первом счету ему начисляли 7% годовых, а на втором – 8% годовых. Через год он получил 222 грн прибыли....
Dasha555511111 Dasha555511111  03.11.2020 16:23
В одном котле налито Пузырьковое Зелье, в другом таком же котле Кока - Кола. Из котла с зельем перелили один половник к кока - Коле и размещали. Затем такой же половник смеси...
Parf21 Parf21  03.11.2020 16:23
Cos х = 0; 2) sin x = - 1; 3) sin x =1​ помагите с Алгеброй...

Популярные вопросы