1. Алгебра
  2. Розв яжіть рівняння (x^3)+2x=sinx

Розв'яжіть рівняння (x^3)+2x=sinx

вовчик83 вовчик83    3   09.05.2020 00:56    0

Ответы
AirinMandarin AirinMandarin  14.10.2020 12:12

x^3+2x=\sin x

Перший корінь одразу видно: це 0 (бо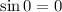 \sin 0=0).

Доведемо, що інших коренів немає. Щоб їх не було, функція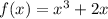 f(x)=x^3+2x має рости (або спадати — тут це неважливо, бо обидві функції непарні) швидше, ніж функція 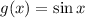g(x)=\sin x на всій області визначення (тобто її похідна має бути більшою) Знайдемо похідні обох функцій:

f'(x)=3x^2+2\\g'(x)=\cos x

Доведемо, що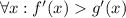 \forall x: f'(x) g'(x), тобто 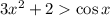3x^2+2 \cos x. Це випливає з того, що 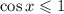\cos x \leqslant 1 (за означенням косинуса), а 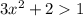3x^2+21 (доведемо це):

3x^2+21\\3x^2-1\\x^2-\dfrac{1}{3}

Квадрат виразу не може бути від'ємним на множині дійсних чисел, тому нерівність доведено.

Відповідь: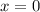 x=0.


Розв'яжіть рівняння (x^3)+2x=sinx
Розв'яжіть рівняння (x^3)+2x=sinx
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Elnarikys Elnarikys  26.05.2019 00:40
Найдите смежные углы, если один из них на 42(градуса) меньше другого...
korolevaleksan korolevaleksan  26.05.2019 00:40
Кисть, которая стоила 240 рублей, продаётся с 25%-й скидкой. при покупке двух таких кистей покупатель отдал кассиру 500 рублей. сколько рублей сдачи он должен получить?...
rminichkina rminichkina  26.05.2019 00:40
√4а; √25b; √16с; √49d вынесете множитель из знака...
Tytiki Tytiki  26.05.2019 00:40
Найдите наибольшее значение функции у = -х^2 +6х - 4...
Дуся003 Дуся003  26.05.2019 00:40
Не выполняя постороения , определите , пересекаются ли парабола у= 1/5 х^2 и прямая у=20 -3х . если точки пересечения существуют , то найдите их координаты ....
julealeo julealeo  26.05.2019 00:40
Розвязати подвійну нерівність -3,5 менше 4х+1\2менше рівне 2,5...
Лерапомогите1 Лерапомогите1  26.05.2019 00:40
Вычислите b^(log(5)корень из 7) если 7^(log(5)b)=4 варианты ответов: a 2 b3 c1 d4 e5...
nikakrasovska nikakrasovska  26.05.2019 00:40
Разложите на множители : (а-х) у (в третьей степени) -(а-у) х(в третьей степени) + (х-у) а(в третьей степени) (всё это одно выражение)...
УмнаяДебилка УмнаяДебилка  26.05.2019 00:40
1.на оси абсцисс найдите точку, расстояние от которой до точки м (3; -3, 0) равно 5. 2.во время параллельного переноса точка а (2, -1, 3) переходит в точку а1 (3; -2, 1)....
albinanizaeva albinanizaeva  26.05.2019 00:40
Найдите сумму трех последовательных нечетных чисел, меньшее из которых 2n+7....

Популярные вопросы