Розв'язати квадратне рівняння
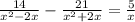
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычислите выбирая удобный порядок действий а) 25*197*4= б) 8*567*125= в) 50*23*40=...
2 - Сумма квадратов четырех последовательных непарных чисел=276. найти эти числа...
3 - Сдесятиградусного мороза принесли кусок льда массой 3,5 кг. какое количество теплоты...
2 - При каком условии около четырёхугольника можно описать окружность?...
2 - Укажите формулу оксида который при обычных условиях является жидкостью а) so2...
1 - Площадь основания правильной треугольной призмы вдвое меньше площади боковой грани....
2 - Найти производную: y=корень из x(3x-1)...
1 - Составить 4 сложных предложения с прилагательными, которые бы подошли под следующие...
1 - Present perfect or present perfect contiuous . 1)i can t open the door. i ) my...
1 - Найти производную: y=tg* корень из sin3x...
2
Смотри решение на фото
х≠2, х≠-2, х≠0
Решим с дискриминатом
х1=-5
х2=3,6