Решите уравнения , сейсас на паре надо
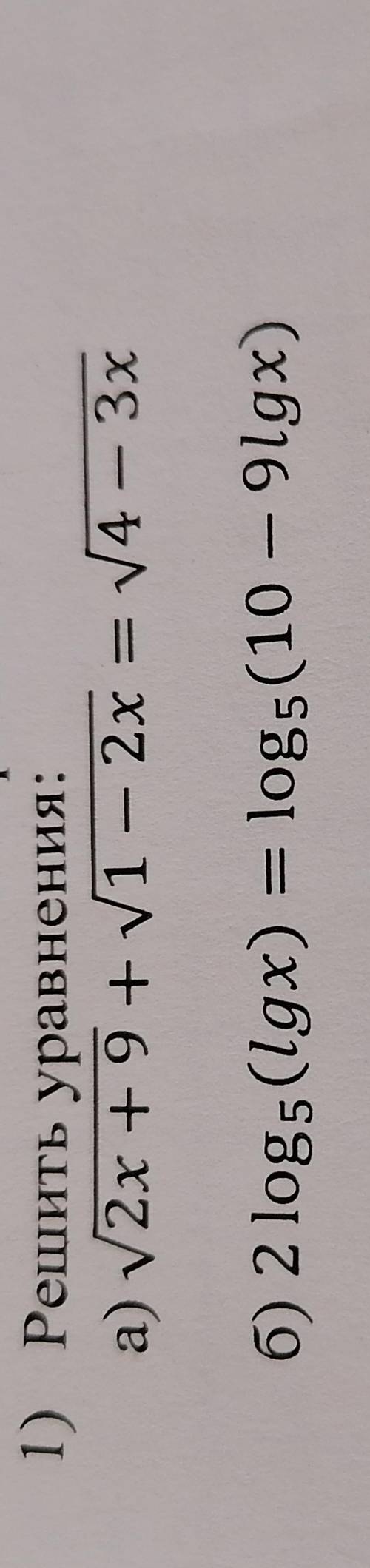
Другие вопросы по теме Алгебра
Популярные вопросы
- Найди значение выражения.ответ:НазадПроверить...
2 - ть будь ласка твір мініатюра на тему чого навчає нас сучасників твір...
2 - знайдіть площу основи правильної чотирикутної піраміди, висота якої...
3 - 34 Я – ученик.Я – ученицаВ. Голявкин«Рассказы»пиши имена героев рассказов...
2 - Какими цифрами на картинке обозначены: артезианская скважина — ; межпластовые...
2 - Высшей добродетелью выдающийся китайский философ Конфуций признавал:...
1 - Дан участок молекулы ДНК : -ГГА-ТЦГ-ТАЦ-ЦТА-АГГ-… Определите аминокислоты...
3 - Работа в группах. 211. Спишите, вставляя пропущен-ные буквы в местоимениях...
2 - Read and complete .Use a,an,the where necessary....
2 - Найди координаты точки пересечения графика функции y = x — 2с осью...
3
1
ОДЗ:
Проверка:
ответ: -4
2.
ОДЗ:
Второй корень не входит в ОДЗ
ответ: 10