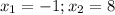Решите уравнения. Г, Д, Е.

Другие вопросы по теме Алгебра
Популярные вопросы
- 1. Даны точки А(-1; 2), В(3;0) и С(1;2). Найти: 1) координаты векторов...
3 - Сделайте ПРАВИЛЬНО И ПОДРОБНО...
1 - Очень практическая работа по географии...
3 - Упр 349. Части слов потеряли друг друга. Если их прочитать от-дельно,...
2 - Очень-очень с литературой нужно написать сочинение на тему Актуальность...
2 - разложите на множители. Если можно, то с объяснениями откуда то или...
2 - Проблеми та образи порушені в поемі Іван Підкова....
2 - Приветствую тебя, надеюсь ты сможешь это сделать...
2 - Тезисы: 1)Чацкий-человек ума и чувства 2)Идеал Чацкого(требование)...
1 - Переліку формул: C2H5OH, HCOOH, CH3CH(CH3)COH, CH3CH2COOH, CH(CH3)2CH2COOH...
1
г) x = 18
д) корней нет
е) x1 = 8
x2 = -1
Объяснение:
г) x^2 - 36x + 324 = 0
D = (-36)^2 - 4 * 1 * 324 = 1296 - 1296 = 0
т.к дискриминант = 0,значит в уравнении один корень
x = 36/2 = 18
д) 2x^2 + x + 16 = 0
D = (1)^2 - 4 * 2 * 16 = 1 - 128 = -127
т.к дискриминант отрицательный - корней нет
е) (x^2 - 7x) / 8 - 1 = 0
домножим всё уравнение на 8
x^2 - 7x - 8 = 0
D = (-7)^2 - 4 * 1 * (-8) = 49 + 32 = 81 (9)
x1 = (7 + 9)/2 = 16/2 = 8
x2 = (7 - 9)/2 = -2/2 = -1
г)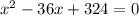
ответ: х=18
д)
ответ: нет действительных корней.
е)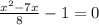
ответ: