Решите уравнения: 4^x- 14*2^x -32=0 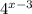 =
= 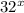
9∧√x-5 - 27=6*3∧√x-5
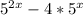

Другие вопросы по теме Алгебра
Популярные вопросы
- 9,3+(3,1-y)=12,2 (решите уравнение)...
2 - Для приготовления салата нужно купить равные части перца, помидоров, огурцов...
3 - Как распределить в 4 букеты 14 желтых и 14 белых астр так, чтобы в каждом...
1 - Цепочки уравнений. n(2)-n(2)o(5)-nano(3)-hno(3)-ca(no(3))2 n(2)o(5)-mg(no(3))2-mg(oh)2-mgo...
2 - Выполни деление с остатком по плану и проверь решения...
3 - На дворе горой, а в избе водой. отгадай ее. обозначь в словах ударения....
1 - Как правильно видать или видеть или видить и какое спрежение...
2 - Постройте равнобедренный треугольник авс, в котором ав=вс=13 см, ав=12 см,...
2 - Сообщение о ростове.окруж мир 3класс...
3 - Пальто стоит 64000 рублей.вначале его цена упала на 10%а затем на 1800 рублей.на...
2
1)
Введём замену: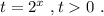
По теореме Виета:
Но так как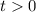 , то -2 не является решением этого уравнения. Выполняем обратную замену:
, то -2 не является решением этого уравнения. Выполняем обратную замену:
ответ: 4.
2)
ответ: -2.
3)
Введём замену:
По теореме Виета:
Но так как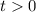 , то -1 не является решением этого уравнения. Выполняем обратную замену:
, то -1 не является решением этого уравнения. Выполняем обратную замену:
ответ: 1.
4)
ответ: 1.
5)
Для начала кое-что учтём: подкоренное выражение всегда неотрицательно. То есть:
Продолжаем решение:
Введём замену: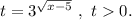
По теореме Виета:
Но так как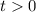 , то -3 не является решением этого уравнения. Выполняем обратную замену:
, то -3 не является решением этого уравнения. Выполняем обратную замену:
ответ: 9.