Решите уравнение
Есть ещё примеры щас задам ещё 1 вопрос
Дробно рациональные уровнения
Другие вопросы по теме Алгебра
Популярные вопросы
- Справедливы ли следующие утверждения: 1) произведение 24*73 делится...
1 - Длина комнаты на 2,39 м больше ее ширины, а ее периметр равен 14,06...
1 - Число х равно сумме первых 20 натуральных чисел, а у равно сумме первых...
1 - Из отрезка [1; 3] выбирают натуральное число а. Из интервала (45; 52)...
2 - Каждое ребро куба увеличили на 40%. На сколько процентов увеличился...
1 - Отправившись в лес за грибами, Юра собирал только белые грибы, подберезовики...
2 - х - натуральное число из интервала (2; 6), а натуральное число из интервала...
3 - К празднику организация приобрела 3 упаковки роз по 125 штук в каждой...
3 - Родители купили для школьного праздника 21 коробку конфет по 55 конфет...
3 - Каково наименьшее натуральное число, 20% которого больше, чем 1,2?...
1
а)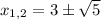
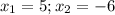
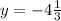
б)
в)
Объяснение:
а)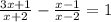
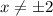
ОДЗ (знаменатели не равны нулю):
б)
ОДЗ (знаменатели не равны нулю):
в)
ОДЗ (знаменатели не равны нулю):