Решите уравнение x(2)+3x-54=0 решите уравнение 4x(2)-9x=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите сокращенную форму: 1. i am not at home. 2. i was not at school....
3 - Составить 5предложений с деепричатиями и 5 предложений с причастиями)) кто...
3 - Наркомания свидетельство неблагополучия в стране.как вы думаете,почему же...
3 - Необходимо начертить ломаную с 3 равными звеньями так, чтобы ее длина была...
1 - Впараллелограмме один из двух углов, прилежащих к одной стороне, на 250%...
3 - Около треугольника авс описана окружность с центром о. найти угол воа, если...
1 - Периметр прямоугольника равен 28 м. а его площадь 48 м в квадрате. найти...
2 - Решить по информатике. задан массив случайным образом.преобразовать массив:...
2 - Маша купила 8 тетрадей в линейку и х тетрадей в клетку. сколько тетрадей...
3 - Фотон электромагнитного излучения имеет энергию 6,4*10(в -19) дж. определить...
2
а).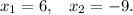
б).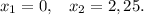
Решение:а). Решим первое уравнение:
б). А теперь - второе:
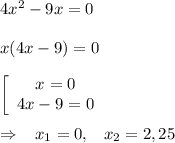
Примечание:а).
Здесь мы пользовались формулой корней квадратного уравнения: если мы имеем уравнение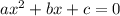 , то корни
, то корни 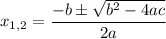 , где
, где 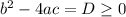 .
.
б).
Здесь мы просто разложили на множители и воспользовались более простым фактом: если произведение нескольких чисел равно нулю, то хотя бы одно из них равно нулю.