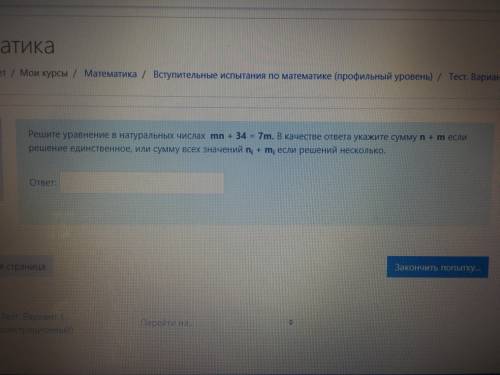
Решите уравнение в натуральных числах

ответ: 62.

Объяснение:

Перепишем уравнение в виде m*n-7*m=-34, или m*(n-7)=-34. Так как m>0, то число n-7 должно быть отрицательным. А так как и n>0, то это возможно лишь при n=1,2,3,4,5,6. Но если n=1,2,3,4, то число m не является натуральным, поэтому эти значения не годятся. При n=5 находим m=17, а при n=6 m=34. Таким образом, найдены две пары решений: m1=17,n1=5,m2=34,n2=6. Отсюда m1+n1=22, m2+n2=40 и тогда искомая сумма S=22+40=62.