Решите уравнение:
+(tgx)^2=2
Другие вопросы по теме Алгебра
Популярные вопросы
- У рівнобедреному трикутнику ΔCBA основа BA дорівнює 16 бічної сторони....
1 - Нужно полное решение заданий с 1,2...
2 - -2, 5 а в кубе в в квадрате, если а=-2, в=5...
2 - решить. В равнобедренном треугольнике MNP с основанием МР угол М=43 градуса....
2 - Знайти суму,доданками якої є числа:обернене і протилежне числу 2,8,до...
1 - , укажите где ошибка в чертеже соединения винтом и как сделать правильно?...
3 - укр у склі (nc=1,5) довжина світлової хвилі дорівнює 350 нм. при переході...
2 - При дієприслівникові є залежні слова в реченні (розділові знаки вилучино)...
3 - Как относился к русскому народу и Левше атаман Платов и Александр1 ? Вопрос...
1 - Нахождение значения функции по значению аргумента и наоборот. Урок 2 Укажи...
1
Применим формулу (1) в данное уравнение
Пусть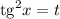 получаем
получаем
Решая как квадратное уравнение (через дискриминант), получим
Выполним обратную замену