1. Алгебра
  2. Решите уравнение [tex]

Решите уравнение
\frac{3}{x + 5} + 1 = \frac{10}{ {x}^{2} + 10x + 25 }

AnnaSind AnnaSind    3   08.08.2019 21:20    0

Ответы
ArtyomFoshan ArtyomFoshan  04.10.2020 05:54

\frac{3}{x+5} +1=\frac{10}{x^2+10x+25}\\x^2+10x+25 = (x+5)^2\\\frac{3}{x+5} +1=\frac{10}{(x+5)^2}\\\frac{1}{x+5}=t;\\3t+1=10t^2\\10t^2-3t-1=0\\D = 9 + 40 = 49\\t_1 = \frac{3+7}{20} = 0.5\\t_2=\frac{3-7}{20}=-0.2\\\frac{1}{x+5} = t_1\\\frac{1}{x+5} = 0.5\\x+5 = 2\\x = -3\\\frac{1}{x+5} = t_2\\\frac{1}{x+5} = -0.2\\x+5 = -5\\x = -10\\Answer: \\-3\\-10

ПОКАЗАТЬ ОТВЕТЫ
Виктория10000000 Виктория10000000  04.10.2020 05:54

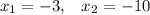
ответ:  x_1=-3,\;\;\;x_2=-10

\displaystyle \frac{3}{x+5} +1=\frac{10}{x^2+10x+25}\\\\\frac{x+8}{x+5}=\frac{10}{(x+5)^2}\\\\10(x+5)=(x+8)(x+5)^2\\\\(x+8)(x+5)^2-10(x+5)=0\\\\(x+5)((x+8)(x+5)-10))=0\\\\(x+5)(x^2+13x+30)=0

Произведение двух чисел равно нулю только тогда, когда одно из низ равно нулю. Поэтому:

\left[\begin{array}{ccc}x+5=0\\x^2+13x+30=0\end{array}\right \\\\\left[\begin{array}{ccc}x=-5\\\left[\begin{array}{ccc}x_1=-3\\x_2=-10\end{array}\right \end{array}\right

Но теперь необходимо проверить, дают ли эти числа нули в знаменателях.

Первый корень явно не подходит (в первой дроби: -5 + 5 = 0). А второй и третий корни подходят!

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
nadezdaakopan nadezdaakopan  07.06.2019 11:00
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. команда «» играет три матча с разными . найдите вероятность того, что...
Vikusya18101 Vikusya18101  09.12.2020 08:34
(15n-2)-(7n-26) кратно 8 при любом натуральном значении n...
кирилл2127 кирилл2127  09.12.2020 08:34
Зведіть многочлен до стандартного вигляду:10x^2-(2x-9)(5x+3)​...
pikuss pikuss  02.09.2019 20:30
Укажите решение неравенства х²-81 0...
Mashavyd Mashavyd  02.09.2019 20:30
Один из углов паралелограма равен 102 градусов найдите меньший угол этого паралелограма ?...
ВИКУСИК4455 ВИКУСИК4455  02.09.2019 20:30
1.разложите многочлен а^3-4а^2-4а+16 на линейные множители 2.выполнить умножение многочленов (m-n+1)(m+n+1) 3.найдите такой одночлен p,при котором многочлены с^2-a и (с^3-2а^3+2a^2c^2-ac)*p^-1...
wagnercop06s12 wagnercop06s12  02.09.2019 20:30
Решите при х=1 2х^2-3х х дробная черта : х-2 х-2...
НяшнаяПанда НяшнаяПанда  02.09.2019 20:30
Объясните, , почему решением данного квадратного неравенства 1 4х^2 является (-бесконечность; -0,5) u (0,5; +бесконечность) а не ( -0,5; 0,5)....
TanyaVasutina TanyaVasutina  02.09.2019 20:30
1. найдите значение выражения 7,7 - 5,3....
Lafemme1 Lafemme1  02.09.2019 20:30
Первый рабочий за час делает на 9 деталей больше чем второй и выполняет заказсостоящий из 122 деталей на4 часа быстрее чем второй рабочий выполняющий такой же заказ. сколько деталей...

Популярные вопросы