Решите уравнение
} - 2 * 0.25^{\frac{sin^{2}(x-\frac{pi}{4})}{cos2x}} - 1 = 0)
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычисли площади четырёхугольников (задание в фото)...
3 - чи могли люди за первісних часів жити і працювати окремо а не колективом?...
3 - 47. Сосчитайте постоянную времени цепи, состоящей из конденсатора емкостью...
1 - Кушан шаруашлыгы комектесинишши...
1 - А) Запишите только средства связи предложений в следующих текстах, текст переписывать...
1 - Придумайте стихотворение на день рождение для мамы только не берите из интернета...
3 - 1) вывод о географическом положении Египта ; 2) вывод значения Египта в мире...
1 - вычислите массу негашеной извести (CaO) которая получается при обжиге 300...
1 - в чем отличие литературной сказки от народной а в чем сходство используй опорные...
2 - В. Начальная концентрация вещества А равна 0,22 моль/л, а через 10 c — 0,201...
1
Решение приложено
=========================================================
ОДЗ:
Замена: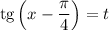
ответ: нет действительных корней.