1. Алгебра
  2. Решите уравнение: sin 2x

Решите уравнение: sin 2x = 2 cos^2 x. найдите решение на отрезке [-0,5п; 1,5п].

мирэлюзий мирэлюзий    1   25.07.2019 22:10    2

Ответы
ЛераТян2000 ЛераТян2000  03.10.2020 13:03

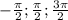а) \frac{\pi }{2} +\pi n,~n\in\mathbb {Z}; \frac{\pi }{4} +\pi k,~k\in\mathbb {Z};    б) -\frac{\pi }{2} ; \frac{\pi }{2}; \frac{3\pi }{2}; \frac{\pi }{4} ; \frac{5\pi }{4}.

Объяснение:

sin2x=2cos^{2} x

Воспользуемся формулой sin2x=2sinxcosx

2sinxcosx-2cos^{2} x=0;\\2cosx( sinx-cosx) =0;\\\left [ \begin{array}{lcl} {{cosx=0,} \\ {sinx-cosx=0;}} \end{array} \right.\Leftrightarrow \left [ \begin{array}{lcl} {{cosx=0,} \\ {tgx=1;}} \end{array} \Leftrightarrow\right.\left [ \begin{array}{lcl} {{x=\frac{\pi }{2} +\pi n,~n\in\mathbb {Z}} \\\\ {x=\frac{\pi }{4}+\pi k, ~k\in\mathbb {Z}}} \end{array} \right.

Выберем корни , принадлежащие отрезку  [-\frac{\pi }{2} ; \frac{3\pi }{2} ]

Из первой серии это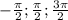 -\frac{\pi }{2} ; \frac{\pi }{2}; \frac{3\pi }{2}

из второй \frac{\pi }{4} ; \frac{5\pi }{4}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
200939 200939  17.05.2019 23:20
Чтобы выложить пол в ванной комнате, потребуется 180 маленьких квадратный плиток или 80 больших. сторона большой плитки на 5 см больше, чем сторона маленькой. какова...
zemkina347 zemkina347  17.05.2019 23:20
У=х в 4 степени,построить график функции....
Sghkllhcx Sghkllhcx  17.05.2019 23:20
У=х во 2 степени ,нужно построить график функций....
269069 269069  17.05.2019 23:20
1)сколько граммов соли содержится в 100 граммах 13%-го водного раствора соли?...
Лол11лол Лол11лол  17.05.2019 23:20
Cократите дробь: 3a(a+b)2 9a2(a+b) где, (a+b) (всё во 2-ой степени) где, 9a2 (девять a во 2-ой степени)...
AmmosD AmmosD  17.05.2019 23:20
F(x)=2x^3-3x^2-12x+8 найти экстремумы...
annzhoravel461 annzhoravel461  17.05.2019 23:20
__ докажите ,что : х5 делится нацело на 5 ....
FannyPanda FannyPanda  17.05.2019 23:20
Найдите значение дроби: 15а2 - 10ab 3ab - 2b2 при a = - 2; b = - 0.1 там где 15a2 (пятнадцать a во 2 степени); 2b2 (два b во 2 степени)...
Nematzoda1999 Nematzoda1999  17.05.2019 23:20
Садоводы собрали 85 тонн яблок трёх сортов. мяса яблок первого сорта составляет 45% массы яблок второго сорта, а масса яблок третьего сорта составляет 5/9 массы яблок...
влад2299 влад2299  17.05.2019 23:20
Вмагазин 9 тонн картофеля. в первый день продали 1/3 всего картофеля, во второй - 2/3 остатка. в третий день продали остальной картофель. сколько тонн картофеля продали...

Популярные вопросы