Решите уравнение с решением
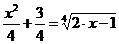
Другие вопросы по теме Алгебра
Популярные вопросы
- Существует ли четырехугольник в котором стороны относятся 2:4:7:9С подробным...
3 - Напиши про 1 любой фразиалагизм...
3 - будь ласка будь ласка будь ласка...
1 - Казахстаннын Жеты кереметы Эссе 80-100соз...
3 - Революция 1848 года во Франции «Народ не только достоин представлять себя,...
2 - Формула потенциала гравитационного поля...
2 - Классифицируйте виды горных пород магматические метафорные осадочные...
2 - Определи порядок выполнения действий и вычисли...
2 - 5. Какой литературный персонаж мог бы собрать это бинго? Напишите её имя....
1 - 2. Приведите дроби к знаменателю 36: а) 1/3 б) 3/4...
2
x=1
Объяснение:
рассмотрим функцию:
2x-1≥0 ⇔ x≥0.5
Её область определения: D(f)=[0.5;+∞)
Исследуем ее с производной:
Находим нули числителя:
Замечаем, что слева стоит возрастающая функция, справа - убывающая. Поэтому если и есть корень, то он единственный!
Не трудно догадаться, что корнем будет x=1
Теперь находим нули знаменателя:
метод интервалов с учетом D(f)
(0,5)---[1]---->ₓ
С пробных точек узнаем знаки промежутков и получаем:
(0,5)---[1]+++>ₓ
На интервале (0,5;1) производная отрицательна, значит функция убывает.
На интервале (1;+∞) производная положительна, значит функция возрастает
Таким образом x=1 - точка минимума и в том числе точка наименьшего значения функции
f(1)=0 - минимум и наименьшее значение функции
Таким образом мы выяснили, что f(x)≥0 при всех допустимых x, а равенство f(x)=0 достигается только в точке x=1 (в точке минимума)