1. Алгебра
  2. Решите уравнение с подробным

Решите уравнение с подробным решением.

Evgsolnce Evgsolnce    1   08.07.2019 17:01    1

Ответы
drxayala1 drxayala1  16.09.2020 18:02

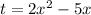
\sqrt{2x^2-5x+12}+2x^2-5x=0

Пусть t=2x^2-5x

\sqrt{t+12}+t=0\\\sqrt{t+12}=-t\\\left \{ {{t+12=t^2} \atop {t\leq 0}} \right. \left \{ {{t^2-t-12=0} \atop {t\leq 0}} \right. \left \{ {{t=-3;4} \atop {t\leq 0}} \right. \Rightarrow t=-3\\2x^2-5x=-3\\2x^2-5x+3=0

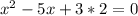Уравнение x^2-5x+3*2=0 имеет корни 2 и 3, значит, исходное уравнение имеет корни 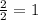\frac{2}{2}=1 и \frac{3}{2}.

ответ: 1; 1,5

ПОКАЗАТЬ ОТВЕТЫ
Macsoneo Macsoneo  16.09.2020 18:02

Решение во вложении. Удачи в учёбе,мой друг!

P.S. Выражение с корнями не подходит, так как вычисляется приближенное значение.


Решите уравнение с подробным решением.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
НикитаЗеленюк НикитаЗеленюк  31.08.2019 01:50
2x+4y=-5 построить график уравнений...
viloxy viloxy  31.08.2019 01:50
Нужна sin^2x+sin^2*pi/6=cos^2*2x+cos^2 * pi/3...
влад2318 влад2318  31.08.2019 01:50
1) корень из 2х^2 -5х+1(конец корня)= х-1 уравнение 2) сократить дробь , личник: корень 8 степени из лика а - (минус) корень 8 степени лика b. назоуник: корень...
maxim1804 maxim1804  31.08.2019 01:50
Решить тригонометрические уравнения( ): 1) 2) 3)...
valentinateleg2607 valentinateleg2607  05.06.2019 22:00
Квадраты (2x+3y)^2 (3a-2b)^2 (4u-3t)^2 (2m+1\2n)^2 (ab+2)^2 (x-1\x)^2 (y+1\y)^2 (1-xz)^2 решение: 3 1/2- дробь - степень...
Enjoy167 Enjoy167  05.06.2019 22:00
1. в классе 20 учеников. учитель решил проверить работу у 6 из них. сколько существует выбрать учеников для проверки? 2. найдите вероятность того, что все буквы...
sirghost743 sirghost743  05.06.2019 22:00
Шахматный слон может за один ход перейти на любое число полей, двигаясь только по диагонали. шахматный слон случайным образом поставлен на доску. найдите вероятность...
MomoiSatsuki16 MomoiSatsuki16  05.06.2019 22:00
Построить график функции у=0,4х-8 и по нему найти: при каком значении х значение у равно -8; -2; 0; 0,5; 1,5; 4....
оооооченьТупой оооооченьТупой  05.06.2019 22:00
Разложите на множители 2b в кубе +54...
miragrrr miragrrr  09.12.2021 21:47
Определить, сколько целых решений имеет неравенство на интервале(0;2n). с пошаговым решением...

Популярные вопросы