1. Алгебра
  2. Решите уравнение методом выделения

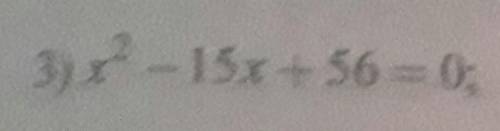
Решите уравнение методом выделения полного квадрата


Решите уравнение методом выделения полного квадрата

Кара101 Кара101    3   14.02.2021 08:18    1

Ответы
katya1074 katya1074  16.03.2021 08:27

Объяснение:

x²-15x+56=0; Домножим в середину многочлена 2 и 1/2 чтобы выделили квадратную формулу (а-b)²=a²-2ab+b²:

x^2-2*\frac{15}{2}*x+56=0

наш второй член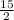 \frac{15}{2}, a значить мы должны прибавить 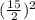(\frac{15}{2})^2 и чтобы уравнение не изменилось мы должны отнять это же число, то есть:

x^2-2*\frac{15}{2}*x+(\frac{15}{2})^2-(\frac{15}{2})^2+56=0 теперь у нас полная формула (а-b)²

(x-\frac{15}{2})^2-\frac{225}{4}+56=0\\ переносим числа в левую часть с противоположными знаками:

(x-\frac{15}{2})^2=\frac{225}{4}-56\\

(x-\frac{15}{2})^2=\frac{225}{4}-\frac{56*4}{4}=\frac{225-224}{4}=\frac{1}{4}\\

теперь в обих частях вычеслим квадратный корень:

x-\frac{15}{2}=\frac{1}{2} и x-\frac{15}{2}=-\frac{1}{2}

x=8; x=7

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
цыпабезума цыпабезума  02.04.2019 13:48
При каком значении n ,(n-натур-е число),значение выражений n^2 , 2n+3 , 3n+4 , n^2+n+7 будут последовательными членами арифметической прогрессии .найти эти члены .​....
uikyky uikyky  02.04.2019 13:42
Найдите наибольшее целое положительное решение системы...
Lololo567 Lololo567  02.04.2019 13:38
Три команды играли в игру. в первый день победили на 5 монстров меньше, чем и в 2 раза меньше, чем в этот не могу понять свою ошибку, какие числа вписать?...
шпион223709 шпион223709  21.06.2019 12:40
6/x-2+5/x=3 решить уравнение с дискриминантом, ничего не могу понять в этих уравнениях , ,напишите с объяснением если можно. огромное...
Sonya112 Sonya112  21.06.2019 12:40
1.найдите второй двучлен в разложении на множители квадратного трёхчлена 6х^2-42+60=6(х- 2.найдите второй двучлен в разложении на множители квадратного трёхчлена 5х^2-45+5(х-...
юлия1913 юлия1913  21.06.2019 12:40
Теплоход вмещает 750 пассажиров и 25 членов команды.каждая шлюпка вместить 70 человек.каково наименьшее кол-во шлюпок,в которых можно разместить всех пассажиров и команду...
anyagabova anyagabova  21.06.2019 12:40
Теория вероятности в коробке лежат 5 черных и 2 красных шара. наугад вынимаются 2 шара. найти вероятность того, что вынуты: а) два черных шара; б) два красных шара; в) шары...
meriko2 meriko2  01.12.2020 10:23
Решите уравнения: а) х²=3; б) х² = - 3; в) х² – 2,25 =0 .​...
Dimalchik Dimalchik  01.12.2020 10:23
В фирме стоимость (в рублях) колодца из железобетонных колец рассчитывается по формулеC=5000+4500n, где n- число колец, установленных в колодце. Пользуясь этой формулой,...
vaniafatyanov vaniafatyanov  01.12.2020 10:24
Решите два номера6 и 7номер...

Популярные вопросы