Решите уравнение log3 (x-5)=log3 (2x+4)+log1/3 (x+2)
Другие вопросы по теме Алгебра
Популярные вопросы
- Выпишите из текстов сначала сложноподчиненные предложения, части которых...
2 - 11 и объясните . именно эти не понимаю...
1 - Open brackets using past simple or past perfect. 1. the girl (to be glad)...
1 - Назавите как называются эти формулы...
2 - Около окружности описаны правильный треугольник и четырехугольник. периметр...
2 - Прямота отношений катерины к людям в грозе...
3 - При каких изобразительных средствязыка лермонтов рисует картины природы...
3 - 10 словочетаний на тему зимние каникулы...
3 - Составить сочинение на тему рассказ кавказский пленник по плану 1. война...
1 - рассчитайте a) молярные массы эквивалентов указанных элементов в соединениях;...
2
1)ОДЗ: x-5>0 => x>5
x+2>0 => x> -2
Общее: x>5
2)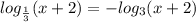
3)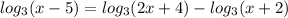
При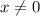 =>
=>
х=7 удовлетворяет ОДЗ (x>5)
ответ: x=7