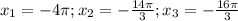Решите уравнение и найдите корни, принадлежащие данному отрезку: cosx=cos2x [-11/2 п; -4п]
Другие вопросы по теме Алгебра
Популярные вопросы
- Надо ! язык! прочитайте опр. спряж.глаг. веять,держать,наклеить,болеть,варить,доказывать,мечтать,смотреть,вертеть,запомнить,ловить,прыгнуть,сверкать,обидеть,беспокоить....
2 - Составьте предложения со словами миллион миллиард,пятьсот,семьдесят три...
3 - Невеликий твір на тему не розум від книг,а книги від розуму створились .будь-ласка...
2 - Упингвинов киль хорошо развит, а у страусов он практически отсутствует. чем обусловлена...
2 - Решите примеры 140 умножить 2 = 280 умножить 3...
3 - Объем шарика 25 см3. определите выталкивающую силу, действующую на этот шарик...
3 - Создать краткое сообщение о пустыне скартинкой ....
2 - Сколько лет у герасима прожила муму...
2 - Довжина лісовоі смуги-3 кма ширина у 5 разів менша за скільки хвилин можна обійти...
2 - Какое можно составить предложение из слов над, тоненькие, крылашками, с, речной,...
2
Находим объединение в x₁ и x₂, следовательно мы получаем: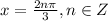 .
.
Теперь находим найдите корни, принадлежащие данному отрезку:
Пусть:
n = -6 ⇒
n = -7 ⇒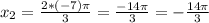
n = -8 ⇒
ответ: