Решите уравнение 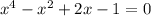и комплексные корни !
методом феррари

(см. объяснение)

Объяснение:

Простейшее разложение на множители!

Метод Феррари не нужен!

Уравнение решено!

х⁴=(х²)²

-х²+2х-1=-(х²-2х+1)=-(х-1)²

(х²)²-(х-1)²=0, по формуле разности квадратов разложим на множители. получим ((х²)-(х-1))((х²)+(х-1))=0⇒х²-х+1=0, дискриминант 1-4=-3

х=(1±√3i)/2

х²+х-1=0⇒x=(-1±√5)/2