Алгебра: Решите уравнение-х^2+4х+3=0

Решите уравнение
-х^2+4х+3=0

Ответы

tibefp33org 19.03.2022 12:50

$\bf \: x_{1} = \displaystyle \frac{ - ( - 4) - \sqrt{28} }{2 \cdot1} = \frac{4 - \sqrt{4 \cdot7} }{2} = \frac{4 - 2 \sqrt{7} }{2} = \frac{ \not2(2 - \sqrt{7}) }{ \not2} = \boxed{2 - \sqrt{7} }. \bf \: \\ x_{2} = \displaystyle \frac{ - ( - 4) + \sqrt{28} }{2 \cdot1} = \frac{4 + \sqrt{4 \cdot7} }{2} = \frac{4 + 2 \sqrt{7} }{2} = \frac{ \not2(2 + \sqrt{7}) }{ \not2} = \boxed{2 + \sqrt{7} }.$

Объяснение:

Умножим обе части уравнения на (-1), чтобы изменить знак коэффициента "а".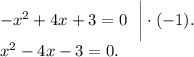

$- x {}^{2} + 4x + 3 = 0 \: \: \: \bigg | \cdot( - 1). \\ x {}^{2} - 4x - 3 = 0.$

Запишем коэффициенты приведённого квадратного уравнения.

а = 1 ; b = –4 ; c = –3.

Запишем формулу дискриминанта:

D = b² – 4 · a · c. Подставим коэффициенты в формулу.

D = (-4)² - 4 · 1 · (-3) = 16 + 12 = 28.

Формулы корней:

$\displaystyle x_{1} = \frac{ - b - \sqrt{d} }{2a} . \: \: \: \: \: x_{2} = \frac{ - b + \sqrt{d} }{2a} . \\$

Подставим коэффициенты и вычислим.

$x_{1} = \displaystyle \frac{ - ( - 4) - \sqrt{28} }{2 \cdot1} = \frac{4 - \sqrt{4 \cdot7} }{2} = \frac{4 - 2 \sqrt{7} }{2} = \frac{ \not2(2 - \sqrt{7}) }{ \not2} = \boxed{2 - \sqrt{7} }. \\ x_{2} = \displaystyle \frac{ - ( - 4) + \sqrt{28} }{2 \cdot1} = \frac{4 + \sqrt{4 \cdot7} }{2} = \frac{4 + 2 \sqrt{7} }{2} = \frac{ \not2(2 + \sqrt{7}) }{ \not2} = \boxed{2 + \sqrt{7} }.$