Решите уравнение f'(x)=0 1) f(x)=sin^2x-sinx+5 2) f(x)=3 cosx + 4sinx - 5z

Во втором примере у Вас опечатка (5z), поэтому рассматриваю 2 случая (под буквами a и b). При этом первый решаю с метода универсальной тригонометрической подстановки, где :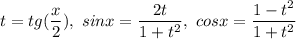

1) f '(x) = 2sinx·cosx - cosx = sin2x -sin (π/2 -x)

f '(x) = 0 ⇔  sin2x  = sin (π/2 -x) ⇔ 2x = π/2 -x + 2πn , n∈Z  или  

 2x = π - π/2 +x + 2πk  ,  k ∈Z  ⇔      

  x = π/6 + 2πn/3 ,  n∈Z  или    x = π/2 + 2πk, k ∈Z  

2) f '(x ) = 4cosx - 3sinx  - 5 = 0 ⇔  4cosx - 3sinx = 5 ⇔    

cosx ·4/5 - sinx·3/5 = 1 ;

Пусть  соsα = 4/5 ;  sinα = 3/5  ; α ∈ ( 0 ; π/2) ;      

 cosx·cosα - sinx·sinα = 1  или :

cos(x + α ) = 1 ⇔ x +α = 2πn ; n ∈Z ⇔  x = - arccos 4/5  + 2πn ; n ∈ Z