Решите уравнение четвертой степени :
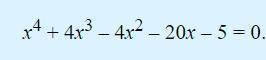
Другие вопросы по теме Алгебра
Популярные вопросы
- Решить систему линейных уравнений a) Методом Гаусса b) Методом Крамера...
2 - Знайти масу Кальцій оксиду, необхідну для з 182,5 г. хлоридної кислоти...
1 - Доведіть, що окунь добре пристосований до життя у воді....
2 - Уменьшите в 3 раз следующие числа...
3 - Знайти периметр п-кутника, якщо у нього всі сторони дорівнюють по 2...
3 - . Если к тем кубикам, которые лежат в коробке, доба- вить еще 8, то кубиков...
1 - Визначити густоту населення Закарпаття ( 1259000 осіб) й порівняти з...
3 - Виберіть правильну відповідь Холмсові вдалося викрити наміри Джона Клея,...
2 - Задание 11 No 1319упростите выражение с квадрате деленное на C в квадрате...
3 - 25 г мідного купоросу розчинили у 175 г води. Обчисліть масову частку...
2
(см. объяснение)
Объяснение:
Произведение равно 0, если хотя бы 1 из его множителей равен 0, а другой при этом не теряет смысла:
Уравнение решено!