Решите уравнение: 7x2+4=2x4 методом замены переменной от
Другие вопросы по теме Алгебра
Популярные вопросы
- Бірде үй өртенді. Өртсөндірушілер әлгі үйге келin жеткенде алдарынан бір әйел...
3 - долго тянет (какая?) полярная ночь. Но и ей приходит конец. В феврале нСкалистый...
3 - 1)Как вы считаете, какой источник более близок к истине: сведения Полиэна или...
2 - Задание Определите природные комплексы, измененные под влиянием антропогенной...
3 - Что понимается под идейным содержанием литературных произведений...
1 - VII Прочтите и устно переведите текст. Перепишите и письменно переведите 1, 2,...
1 - 1. Укажите количество прилага- тельных в 1-й части текста.2. Выпишите в два ряда...
3 - Разложи на множитили многочлен...
2 - A) cos a = 4, АОВ.1013 Найдите ѕіn а, если:125б) cos a = ; в) cos a = -1.23”1014...
2 - Сделать портрет числительных1,15,80,100...
1
x1=2
x2=-2
Объяснение:
ответ: 2
Объяснение:
Пусть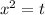 , тогда:
, тогда:
Подставляем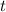 в
в 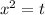 и получаем 2 уравнения:
и получаем 2 уравнения:
Из первого уравнения мы получаем 2 и -2, а из первого мы получаем "нет корней", т.к. корня из отрицательного числа не существует.
ответ: 2 и -2.