Решите уравнение: -5sin 2x - 16(sinx-cosx) + 8 = 0
Другие вопросы по теме Алгебра
Популярные вопросы
- Отметьте верные утверждения по физике...
3 - Почему утиные яйца не продают в магазинах. Какая кухня их использует...
3 - С какой силой взаимодействуют два тела с зарядами 2,5 ·10 -9 Кл и...
3 - это буду показывать по частям. надо сдать через 15 минут...
3 - Ex. 3. Rewrite the sentences in the interrogative form (?) a ) John...
1 - Қуат көзін үнемдей білеміз бе? Сочинение50 слов...
2 - Эссе помыш Жазылым 1. Берілген тақырыптардың бірін таңдап, 120-150...
3 - тесты по истории умоляююю...
1 - . Соленость является одним из свойств вод Мирового океана a. Определите...
2 - очень сильно! Сделайте 2 вариант под цифрой 3)...
1
Пусть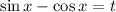 при этом
при этом 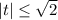 , тогда, возведя в квадрат обе части равенства, получим
, тогда, возведя в квадрат обе части равенства, получим 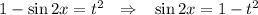
Возвращаемся к обратной замене