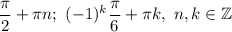Решите уравнение 2sin( п/2 - x) = ctg x
Другие вопросы по теме Алгебра
Популярные вопросы
- Самое большое двузначное число уменьшили на самое маленькое двузначное...
3 - Какие звуки чередуются в корне снеговик...
1 - Составьте словосочитание со словами : белизна, юношество, юнец,...
2 - Конец зависимости руси от орды связан с:...
2 - Используя дополнительный материал напишите короткое эссе не более...
1 - Реальное начало холодной войны 40-х...
2 - Назовите название болезни ног из 5 букв быстрее и : c заранее...
1 - Саша начал выполнять дз в 15 часов 30 мин,а закончил в 16 часов...
3 - This is my dad . he is the head of the family . my dad has brown...
3 - Усерёжи 900р,а у тани 630р.после того как серёжа купил 8 кг конфет,а...
3
ОДЗ: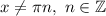
ответ: