Решите уравнение: 2*cos^2*x+3*sin2*x-8*sin^2*x=0

Question

Алгебра: Решите уравнение: 2*cos^2*x+3*sin2*x-8*sin^2*x=0

15kristina · Answer

Разделим обе части уравнения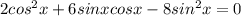 на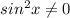 Легко проверить что это выражение в ноль не обращается иначе равенство не выполняется. Тогда уравнение примет вид: Проведем замену: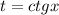 Проведя обратную замену найдем корни исходного уравнения: ;∈ ;∈...

Решите уравнение: 2cos^2x+3sin2x-8sin^2x=0

Популярные вопросы