Решите тригонометрическое уравнение
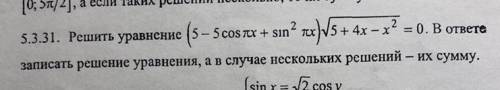
Другие вопросы по теме Алгебра
Популярные вопросы
- Назовите несколько видов хищных птиц и расскажите об их значении в природе....
1 - Какие особенности внешнего строения зверей связаны с их жизнью на суше?...
1 - Какие мышцы наиболее развиты у зверей?...
2 - Назовите органы выделения зверей. Какое значение имеют почки в жизни млекопитающих?...
2 - Какие особенности млекопитающих свидетельствуют о высоком уровне их организации?...
1 - В чём проявляется усложнение дыхательной системы млекопитающих по сравнению с пресмыкающимися...
3 - Каковы особенности строения пищеварительной системы млекопитающих?...
3 - Каковы особенности внешнего строения, скелета и мускулатуры пресмыкающихся и птиц?...
2 - Почему млекопитающие обладают более сложным поведением, чем пресмыкающиеся....
1 - Какие системы органов имеют млекопитающие? Какие функции они выполняют?...
2
получили корень x=2n, затем подставляем любое целое число (это нужно сделать, так как у нас есть ОДЗ, и корни нужно подобрать), получаем только 3 числа, которые ыходят в данный промежуток.
Не забываем про корни квадратного уравнения: -1 и 5.
ОДЗ: подкоренное выражение неотрицательно.-х²+4х+5≥0, х²-4х-5≤0,
По Виету х=-1; х=5
-15
+ - + х∈[-1;5]
При х=-1, х=5, получаем равенство нулю знаменателя.
Установим теперь равенство нулю др. множителя. предварительно преобразовав его 5-5cosπ+sin²πx=0
5-5cosπх+1-cos²πx=0 ; -6+5cosπх+cos²πx=0 ;по Виету cosπх=-6;∅, cosπх=1; πх=2πn; n∈Z; х=2n;Если n=0, то х=0∈ ОДЗ, n=1;х=2;n=2; х=4;n=-1;х=-2∉ОДЗ, Значит, сумма решений уравнения равна
4+2+0+5-1=10