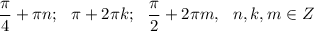Решите тригонометрические уравнения. хотя бы одно! cos(7x)-cos(x)-sin(4x)=0 sin^2(x)+6cos^2(x)+7sin(x)cos(x)=0 4sin^2(x)+5sin(x)cos(x)-cos^2(x)=2 sin(2x)+корень из 2* sin(x-п/4)=1
Другие вопросы по теме Алгебра
Популярные вопросы
- Важнейшие событие при иване антоновича 7 класс дворцовые перевороты...
1 - 3. при взаимодействии этилового спирта массой 9,2 г с оксидом меди (ii)...
2 - Open the brakets to make the story complete....
1 - Что тебе показалось смешным стихотварении с.маршака багаж...
2 - Придумай предложение со словами пуститься наутёк...
2 - Лед выдерживает давление 8 кпа. сможет ли проехать по этому льду овтомобиль...
1 - Построите график функции. найдите координаты точек пересечения графика с...
1 - Со словообразованием. 1.i m afaid i am (care) late 2.the (express) woman...
1 - Придумай предложение со словами пуститься наутёк...
3 - Масса котенка 3/5 а масса щенка1 3/4кг. какими будут показание весов , если...
1
ответ: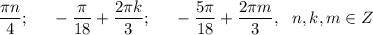
---------------------------------------------------------------------------------------
ответ: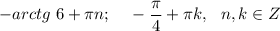
----------------------------------------------------------------------------------------
ответ: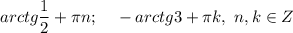
-----------------------------------------------------------------------------------------
ответ: