Решите только г) и д подробно).
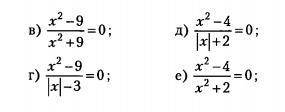
Другие вопросы по теме Алгебра
Популярные вопросы
- 40 . опишите досуг представителей высших слоев xviiiв....
3 - Нужно составить рассказ я в древнем риме когда строили бани...
2 - Решите систему уравнений подстановки: {x+3y=5 {2x-y=3 решите...
3 - Реши . на соревнования приехали 3 группы мальчиков по 6 человек...
3 - Анализ стихотворения б.окуджавы песенка о пехоте !...
1 - Сообщение на тему: животный и растительный мир тропиков.5 класс...
3 - Сын моложе отца на 24 года.через 5 лет отец будет старше сына...
1 - Сочинить сочинение на тему вы совершили свой первый...
1 - Решить неравенство 2sin²x-sinx-3 0...
2 - They always at the lake a)fish b)fished c)fishes d)will fish...
2
Дробь равна нолю, если ее числитель равен нолю, а знаменатель не равен:
В первом уравнении переносим вправо с изменением знака (или вспоминаем формулу разности квадратов:
переносим вправо с изменением знака (или вспоминаем формулу разности квадратов: 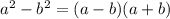 ), а во втором просто переносим
), а во втором просто переносим  вправо:
вправо:
В первом уравнении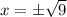 . А решением неравенства
. А решением неравенства 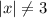 является
является 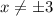 . Иначе говоря:
. Иначе говоря:
Таким образом, все корни, обнуляющие числитель обнуляют и знаменатель (а "делить на ноль нельзя"). Система уравнений получается слишком противоречивой (причем - не кому-то, а самой себе).
Значит, действительных решений у данного уравнения нет.
Это, конечно, можно было и не расписывать так подробно, а просто заметить, что ноль в числителе дают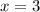 и
и  . Но они же и дают ноль в знаменателе!
. Но они же и дают ноль в знаменателе!
ответ: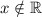 или
или 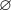
Задание д)Здесь опять: числитель равен нолю, а знаменатель не равен.
Заметим, что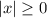 и
и 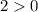 . Значит,
. Значит, 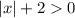 и знаменатель ни при каком значении
и знаменатель ни при каком значении  не равен нолю!
не равен нолю!
⇒ Достаточно, чтобы только числитель был равен нолю.
В общем, это и есть решение уравнения.
ответ: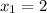 ,
,  .
.
_______________________________________________
Задание в)На всякий случай в) и е). В целом, они решаются абсолютно также, по аналогии, так что мои "объяснения" только испортят красоту решения уравнений.
ответ: ,
, 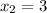
Задание е)ответ: ,
, 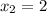
В г) ОДЗ х≠±3; Если х>0, то получим (х-3)(х+3)/(х-3)=0; х+3=0, откуда х=-3;∅, если же х<0, то (х-3)(х+3)/(-х-3)=0;3-х=0;х=3;∅
ответ ∅
е) (х-2)(х+2)=0, умножили обе части на положительное число х²+2, получим х-2=0; х=2; х+2=0; х=-2
ответ ±2
д) разложим на множители, и используем факт равенства дроби нулю, если числитель равен нулю. а знаменатель от нуля отличен.
(х-2)(х+2)=0, когда х=2, проверим знаменатель, модуль двух равен два плюс 2 сумма равна 4≠0, поэтому х=2-корень уравнения. х+2=0; х=-2, т.к. знаменатель не обращается в нуль при подстановки х=-2
ответ х=±2
в) аналогично е) (х-3)(х+3)=0, откуда х=±3, знаменатель число положительное.
ответ ±3