Решите ! $(x - 5) \times (x - 6) - \sqrt{5} \geqslant 0$ ответ получается вроде с дробями.

Ответы

frashthefrash 26.05.2020 15:33

Два решения :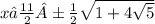 $x≥\frac{11}{2} ±\frac{1}{2} \sqrt{1+4\sqrt{5} }$

Решение в виде обьединения двух неравентсв.

Решение получено так :

$(x-6)*(x-5)-\sqrt{5} =0$

$x^2-11x+(30-\sqrt{5} )=0$

Решаем по формулам.

$D=b^2-4ac=121-4*(30-\sqrt{5} )=1+4\sqrt{5}$

$x(1,2)=(11±\sqrt{1+4\sqrt{5} })$

Преобразуем по формуле (x-x1)*(x-x2)

$(x-\frac{11+\sqrt{1+4\sqrt{5} }}{2} )*(x-\frac{11-\sqrt{1+4\sqrt{5} }}{2} )\geq0$

Решим так: произведение больше либо равно нулю если множители одного знака.

Получим совокупность двух систем, решаем каждую систему и находим два промежутка.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

yana017 15.01.2020 11:52

По заданному графику функции вычислить ее значение...

VolkovaI 15.01.2020 11:54

Аминаgjdhkutdf 15.01.2020 12:03

Kisylyaaa 15.01.2020 12:06

boss23242 15.01.2020 12:10

svetlanasen12 26.08.2020 23:18

11. 1) 7(2a + 1)2 – (3a - 2)(6 - 2a) - 3a2;...

TheDan1lGorbunov 27.08.2020 11:23

Можно с подробный объяснением. Задача на картинке....

Юлия3640 27.08.2020 11:23

X-8 6x+3 решите уравнение ...

Сумасшедшая55555 27.08.2020 11:55

Знайти значення многочлена 2х²-x+4,якщо х=-1,2...

aisasiada 26.08.2020 11:19

Решите ! ответ получается вроде с дробями.​