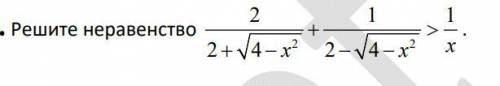
Алгебра: Решите сложное неравенство

Решите сложное неравенство

Ответы

Mesnikfff 15.10.2020 16:20

2/(2 + √(4 - x²)) + 1/(2 - √(4 - x²)) > 1/x

одз x ≠ 0

4 - x² ≥ 0 -2 ≤ x ≤ 2

2 - √(4 - x²) ≠ 0 x ≠ 0

x ∈ [-2,0) U (0,2]

2/(2 + √(4 - x²)) + 1/(2 - √(4 - x²)) = (2(2 - √(4 - x²)) + 2 + √(4 - x²))/((2 - √(4 - x²)(2 + √(4 - x²) = (6 - √(4 - x²))/x²

(6 - √(4 - x²))/x² > 1/x

(6 - √(4 - x²))/x² - x/x² > 0

(x² >=0 отбросим)

6 - x > √(4 - x²)

аналог

системы

4 - x² ≥ 0

6 - x > 0

(4 - x²) < (6 - x)²

-2 <= x <= 2

x < 6

4 - x² < 36 - 12x + x²

2x² - 12x + 32 > 0

x² - 6x + 16 > 0

D = 36 - 4*16 < 0 ветви вверх решение x ∈ R

итак x = одз = [-2,0) U (0,2]

ПОКАЗАТЬ ОТВЕТЫ

pierrotsadclown 15.10.2020 16:20

$\frac{2}{2+\sqrt{4-x^2}}+\frac{1}{2-\sqrt{4-x^2}}\frac{1}{x}\\\sqrt{4-x^2}=a,a\geq 0\Rightarrow \frac{2}{2+a}+\frac{1}{2-a}=\frac{1}{x}\\\frac{a-6}{\left ( a+2 \right )\left ( a-2 \right )}=\frac{1}{x}\Rightarrow x=\frac{\left ( a+2 \right )\left ( a-2 \right )}{a-6}\\\sqrt{4-\left ( \frac{\left ( a+2 \right )\left ( a-2 \right )}{a-6} \right )^2}=a\Leftrightarrow 4-\frac{\left ( a+2 \right )\left ( a-2 \right )}{a-6}=a^2$

$\\\left ( a+2 \right )^2\left ( a-2 \right )^2+\left ( a-2 \right )\left ( a+2 \right )\left ( a-6 \right )^2=0\\\left ( a+2 \right )\left ( a-2 \right )\left ( \left ( a+2 \right )\left ( a-2 \right )+\left ( a-6 \right )^2 \right )=0\\\left ( a+2 \right )\left ( a-2 \right )\left ( a^2-6a+16 \right )=0\Rightarrow a=\pm 2\\a=2\Rightarrow \sqrt{4-4}\neq 2\\D_f=\left [ -2;2 \right ]\setminus \left \{ 0 \right \}$