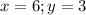1. Алгебра
  2. Решите систему уравнений8x

Решите систему уравнений
8x - 12y = 12
3х +2y = 24​

1DLove11 1DLove11    3   21.05.2021 03:59    0

Ответы
Natasha1146 Natasha1146  20.06.2021 05:02

x=6; y=3

Объяснение:

Данную систему уравнений можно решить банальным методом подстановки, из одного уравнения вычленяя переменную x или y и подставляя ее во второе уравнение.

Но есть и другие решения, я покажу как решить данную систему уравнений методом исключения переменных, что на мой взгляд, гораздо проще с данной системой.

Запишем систему уравнений:

\left \{ {{8x-12y=12} \atop {3x+2y=24}} \right.

Мы можем избавиться от переменной y. Для этого умножаем и правую, и левую части второго уравнения на 6:

3x+2y=24\\6*(3x+2y)=6*24\\18x+12y=144\\

Теперь исключаем переменную y путём сложения двух уравнений. Для начала прибавим второе уравнение системы к первому:

8x-12y+18x+12y=12+144

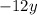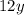Так как сумма двух противоположных величин -12y и 12y равна нулю, удаляем их из нашего выражения:

8x+18x=12+144\\26x=156

Теперь мы легко получаем значение x из данного уравнения:

x=\frac{156}{26}\\x=6

Теперь нам осталось подставить данное значение x во второе уравнение системы:

3x+2y=24\\3*6+2y=24\\

Находим y:

3*6+2y=24\\2y=24-18\\2y=6\\y=\frac{6}{2} \\y=3

Получили ответ: x=6; y=3

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
mamaamamma33 mamaamamma33  08.07.2019 09:10
Найдите значение выражения 12√3*√21*2√7...
Viktor110701 Viktor110701  01.03.2021 17:47
Как решать примеры на подобе таких (x-4) в квадрате, или же (4+b) в квадрате 7 класс...
AlexUnderNewSky AlexUnderNewSky  01.03.2021 17:48
От 339 до 346 номера с решением....
666Лиза66611 666Лиза66611  01.03.2021 17:49
представьте многочлен в виде произведения a в квадрате+ab-3. Упростите выражения -0,4a(2a^2+3)(5-3a^2)...
tanyaparakhina tanyaparakhina  01.03.2021 17:49
1. Дан треугольник KBC. ∠ K = 44°, ∠ B = 38°. Определи величину ∠ C. ∠ C = ? 2. Дан прямоугольный треугольник, величина одного острого угла которого составляет 50°. Определи...
inessaqwerty inessaqwerty  01.03.2021 17:50
Произведение двух натуральных чисел, одно из которых на 5 больше другого, равно 84. Найдите эти числа....
тупая1294 тупая1294  30.04.2020 17:49
-13x+6y=2, найти X через Y; и Y через X....
Leramedvedeva12 Leramedvedeva12  30.04.2020 17:49
Х²+ох+57=0 ,но х1 =3 найти р и х2...
KarinaFelton KarinaFelton  30.04.2020 17:49
6+2418 сократитьТема: Рациональные дроби. Повторение. 1. Сократить дробь: a) 6+2418 b) 2−10+252−25 c) −322−3 2. Выполнить умножение и деление дрбей: a) 2−2⋅2+ b) (2−4)⋅3(+2)2...
vasyapupkin121212 vasyapupkin121212  30.04.2020 17:49
Розв яжіть систему рівнянь 3(х-5)=8у+9 і 7(х+2)-4(у+5)=28....

Популярные вопросы