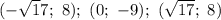Решите систему уравнений сложения х^2 +у^2=81 х^2-у
Другие вопросы по теме Алгебра
Популярные вопросы
- Арифметикалык прогрессиянын бесыншы мушесын немесе n-шы мушесин табындар...
3 - 2-тапсырма:Жазылым. Сан есімнің түрлеріне ажыратып жаз. (Различайте виды имен числительных)...
2 - Колесо велосипедиста имеет радиус 60 см. С какой скоростью едет велосипедист,...
2 - Қызыл кітап туралы эссе жазу...
2 - Сделайте чертеж, выполните задания. Загрузите фото....
1 - Сор по казахскому и 4 тапсырма...
2 - Что вы делаете в своей жизни, чтобы заботиться о Земле? Какие природные опасности...
1 - задание на пресент симпл и пресент пёрфект I (live) with her for 7 years....
1 - Завдання 55. Дайте назви спиртів за їх формулами: а) CH2- CH2 - CH3 I OHб)...
2 - 1.Поезд расстояние в 300 м за 25 с. Определите скорость поезда. 2. Самолет...
3
289 > 0 ⇒ 2 корня
ответ: