1. Алгебра
  2. Решите систему уравнений

Решите систему уравнений методом подстановки:
7х-у=19
2х-9у=-12

Liza200011111 Liza200011111    2   13.12.2021 18:12    4

Ответы
yra8372004 yra8372004  02.02.2022 11:39

\displaystyle \begin{cases}x=3\\y=2 \end{cases}

Объяснение:

\displaystyle \begin{cases}7x-y=19\\2x-9y=-12\end{cases};

В первом уравнении выразим переменную y  через переменную x и подставим полученное выражение во второе уравнение вместо y:

\displaystyle \begin{cases}y=7x-19\\2x-9(7x-19)=-12\end{cases};\;\;

Раскроем скобки и приведем подобные:

\displaystyle \begin{cases}y=7x-19\\2x-63x+171=-12\end{cases}; \\\\ \begin{cases}y=7x-19\\-61x=-12-171\end{cases};

\displaystyle \begin{cases}y=7x-19\\-61x=-183\end{cases}; \\\\ \begin{cases}y=7x-19\\x=-183 :(-61)\end{cases};

Подставим найденное значение переменной x в первое уравнение и найдем значение переменной y:

\displaystyle \begin{cases}y=7 \cdot3-19\\x=3\end{cases};\\\\\displaystyle \begin{cases}y=2\\x=3.\end{cases}

ПОКАЗАТЬ ОТВЕТЫ
Vladchery Vladchery  02.02.2022 11:39

\displaystyle\left \{ {{7x-y=19} \atop {2x-9y=-12}} \right. .

Выразим в первом уравнении переменную "у". Для этого нужно перенести неизвестную в правую часть и сменить ее знак. Получим:

\displaystyle\left \{ {{-y=19-7x} \atop {2x-9y=-12}} \right. \Leftrightarrow\left \{ {{y=-19+7x} \atop {2x-9y=-12}} \right. .

Подставим данное значение "у" в уравнение "2x-9y=-12". Получим:

2x-9\cdot(-19+7x)=-12.

Рапределяем "-9" через скобки. Получим:

2x+171-63x=-12.

Приводим подобные члены. Получим:

-61x+171=-12.

Переносим постоянную в правую часть и сменяем ее знак. Получим:

-61x=-12-171.

Вычисляем разность. Получим:

-61x=-183.

Делим обе стороны уравнения на "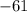-61". Получим:

x=3.

Подставляем данное значение "х" в уравнение "у=-19+7х". Получим:

y=-19+7\cdot3.

Умножаем числа. Получим:

y=-19+21.

Вычисляем сумму. Получим:

y=2.

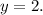
ОТВЕТ: решением данной системы уравнений является пара чисел "(x;y)" \Longleftrightarrow (3;2).
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Dashakrasaveta Dashakrasaveta  08.09.2019 12:30
1.найдите область определения функции y=log(x^2+x+1) y=log(4-x^2) 2.каким соотношением связаны числа m и n, если lg m=1,4153 lg n=3,4153...
vadimkamazurke vadimkamazurke  08.09.2019 12:30
Докажите что функция y=8x-2 является возрастающей или убывающей...
leeJLZeel leeJLZeel  08.09.2019 12:30
Перевести градусы в радианы, 40, 50, 905 градусов в радианы...
vqw80494 vqw80494  08.09.2019 12:30
Найти значение острого угла альфа, если: cos75=cos(90-альфа) вычислить с формулы : cos150 sin135 ctg135 cos120 объясните, как делать это фигню? я вообще ничего не : (...
DeM12345 DeM12345  08.09.2019 12:30
Проходит ли график функции у=-х+3 через точку b(10 -7)...
Sili12 Sili12  08.09.2019 12:30
Перевести 40 град. 50 град. 905 град. в радианы....
Rustem1112 Rustem1112  08.09.2019 12:30
Определите четность или неченость функции f(x)=4x^5+3x^3+x...
Sagi511 Sagi511  12.05.2020 08:46
Пешеход и велосипедист одновременно отправились навстречу друг другу из двух поселков, расстояние между которыми 90 км. Пешеход до встречи с велосипедистом делал остановку на 36...
timofee1999 timofee1999  12.05.2020 08:46
Х^3х^2- 89 х + 231=0 решите...
бооой бооой  12.05.2020 08:47
Найдите произведение корней уравнения 4x^2-28=0. 1) корней нет 2) 7 3) -7 4) корень из 7...

Популярные вопросы