1. Алгебра
  2. Решите систему уравнений:

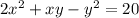
Решите систему уравнений: 2 {x}^{2} + xy - {y}^{2} = 20
​


{x}^{2} - 4xy + 7 {y}^{2} = 13

кира674 кира674    3   16.10.2020 05:19    1

Ответы
1Kolomiets1 1Kolomiets1  15.11.2020 05:19

(3;2)

(-3;-2)

(\frac{17}{2\sqrt{7}};\frac{1}{2\sqrt{7}} )\\(-\frac{17}{2\sqrt{7}};-\frac{1}{2\sqrt{7}} )

Объяснение:

Умножим первое уравнение на 4 и сложим со вторым

9x^{2} +3y^{2} =93\\3x^{2} +y^{2} =31

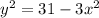Выразим y^{2} =31-3x^{2} и подставим в первое уравнение

2x^{2} +xy-31+3x^{2} =20\\5x^{2} +xy =51

Подставим вместо y его представление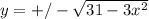  y=+/-\sqrt{31-3x^{2}}

5x^{2} +/-x\sqrt{31-3x^{2} } =51\\+/-x\sqrt{31-3x^{2} } =51-5x^{2}

Возведем в последнем уравнении левую и правую часть в квадрат

x^{2} (31-3x^{2} )=(51-5x^{2} )^{2}

Делаем замену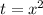 t=x^{2}

В итоге приходим к квадратному уравнению

28t^{2}-541t+2601=0

t_{1}=9 \\t_{2}=\frac{17^{2} }{2^{2}*7 }

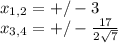
Тогда x_{1,2} =+/-3\\x_{3,4}=+/-\frac{17}{2\sqrt{7} }

Вспоминая, что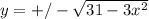 y=+/-\sqrt{31-3x^{2}} находим y

y_{1,2}=+/-2 \\y_{3,4}=+/-\frac{1}{2\sqrt{7} }

Для отбора правильных решений воспользуемся уравнением

5x^{2} +xy =51\\xy =51-5x^{2}

Подставляя вместо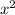 x^{2} его значения 9 и 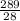\frac{289}{28}, определяем, что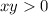 xy0

Значит x и y должны быть одного знака.

(3;2)

(-3;-2)

(\frac{17}{2\sqrt{7}};\frac{1}{2\sqrt{7}} )

(-\frac{17}{2\sqrt{7}};-\frac{1}{2\sqrt{7}} )

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
PoliKotova02 PoliKotova02  03.03.2021 19:53
Квадратный корень. 4 7 9.Заметь, что 7 располагается ближе к 9, чем к 4.Значит, данное число будет лежать на промежутке 2 7 3 бгТеперь аналогично разбери число 11.9...
emin77 emin77  03.03.2021 19:53
Знайдіть найбільше і найменше значення функції y=x8 на проміжку [-2;0]...
Wwwoxanap2013 Wwwoxanap2013  03.03.2021 19:53
Дана функция y + x - 6 x + 5 А Запишите координаты вершины параболы б Определите в каких четвертях находится график функции C Запишите ось симметрии параболы D Найдите...
Victoria200188 Victoria200188  03.03.2021 19:53
2sin A - sin 2 A упростить cos A-1​ ​...
polsedegova polsedegova  20.06.2019 06:00
Втреугольнике авс угол с равен 90 градусов, вс=2, sina= 0, 25. найдите ав....
8877580 8877580  20.06.2019 06:00
Решите неравенство 3х - 2 (х - 5) меньше или равно - 6...
karinatrunko karinatrunko  20.06.2019 06:00
Cos(n+x)=sin n/2 решить уравнение )...
ВалерияГрузд ВалерияГрузд  20.06.2019 06:00
Свежие фрукты содержат 80% воды, а высушеные-30%.сколько сухих фруктов получится из 420кг свежих фруктов?...
сердянечок сердянечок  20.06.2019 06:00
2х^2+x+2=0 это дискриминант решите его формулой d=b^2-4аc...
hakobov2017 hakobov2017  20.06.2019 06:00
Разложить на множители t²-2tb+b² d²-n²...

Популярные вопросы