Решите системное уравнение
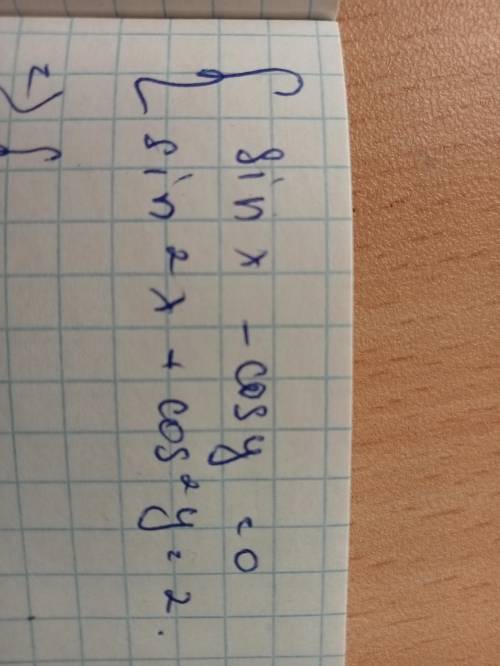
Другие вопросы по теме Алгебра
Популярные вопросы
- Выбери разность квадратов.(Может быть несколько вариантов ответа!)(u+v)2u2−v2(u−v)2(6u+v)2(u−0,8v)236v2−0,64u2...
3 - Мой брат тупой олень не может сделать английский уже долбаный час ему Я не...
3 - НАДО (даю 35б) Сократить: х^2у^2-13х^2у^2+5х^2у^2...
3 - 1)Королевский маршь Львов надо назвать темп, регистр ,тембр2)кенгуру надо назвать...
3 - Продолжите фразу из повести Е. Велтистова. Куда ни посмотришь - везде что-то...
2 - Напишите сочинение, над чем заставила задуматься повесть М. А Булгакова собачье...
3 - О) Составь два подмножества данного мно-жества чисел по самостоятельно установ-ленному...
1 - Найдите в списках лишнюю горную породу : а) гранит,мрамор,алмаз б) уголь,торф,гипс...
2 - Начертите ломаную из 4-х звеньев чтобы её длину можно было найти умножением....
1 - Арларыңның жобасын3-тапсырма. Өздеріңнің болашаққа арналған жоспарлардайындаңдар....
3
Введём две замены: и
и  .
.
Перенесём в верхней части в правую сторону.
в правую сторону.
Теперь выполним подстановку в нижнее уравнение и решим его отдельно.
Получили два значения , теперь для каждого получим значение
, теперь для каждого получим значение  .
.
А теперь выполняем обратную замену.
Получили два решения системы, что и является ответом.
ответ: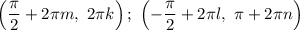 .
.