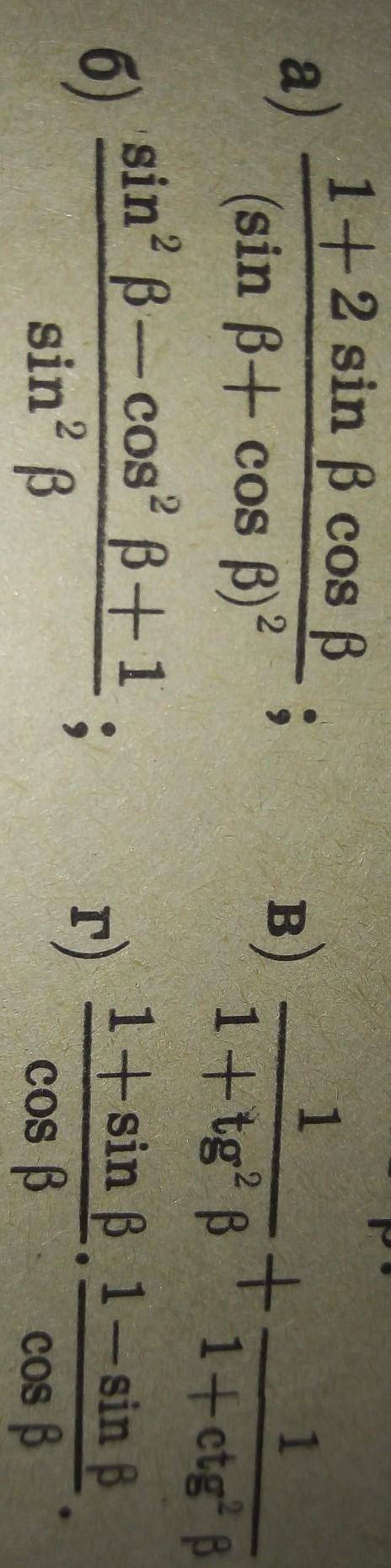
Решите примеры алгебра 10 класс на фото​

Відповідь:

Пояснення:

A) 1+sin2b/sin^2+2sinbcosb+cos^2=

=(1+sin2b)/(sin2b+1)=1

Б) sin^2b+1-cos^2b/sin^2b=

=2sin^2b/sin^2b=2

В) (1+ctg^2+1+tg^2) / (1+ctg^2)(1+tg^2) =

=(2+ctg^2+tg^2) / (1+ctg^2+tg^2+ctg^2*tg^2)

=(2+ctg^2+tg^2) / (1+ctg^2+tg^2+1)=1

Г) 1-sin^2b/cos^2b=cos^2b/cos^2b=1