Решите показательное неравенство и показательную систему уравнений
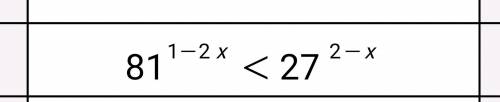
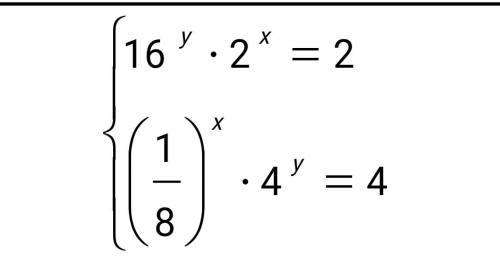
Другие вопросы по теме Алгебра
Популярные вопросы
- Сніговий покрив витримує тиск до 2,5 кПа. Лижнии,на двох лижах, не провалюючись...
2 - № !№21. Составьте схемы предложений с однородными членами, укажите, чем...
2 - Глагол to be. docxглаголы to be ...
2 - Дискретная математика. Отношения....
1 - Составить текст в Past Simple с этими словами на фото минимум 12 слов все...
1 - Складіть порівняльну таблицю Розвиток провідних країн Європи та США...
1 - Какой тип реакции лежит в основе синтеза крахмала и ДНК?...
1 - Мої враження про твір відповідь ззапорожців...
3 - Не понимаю тему. В каждой схеме окислительно-восстановительной реакции определите...
2 - TEXTE Complétez le texte : Je m’appelle Michel. à Toulouse. J’ai 9 ans....
1
Объяснение:
ответ: x∈(-0,4;+∞).
Суммируем эти уравнения:
ответ: (-3/7;5/14).
решение на фотографиях