Решите подстановки систему уравнений : (через Дискриминант)
Пример 3,6.
, очень нужно.
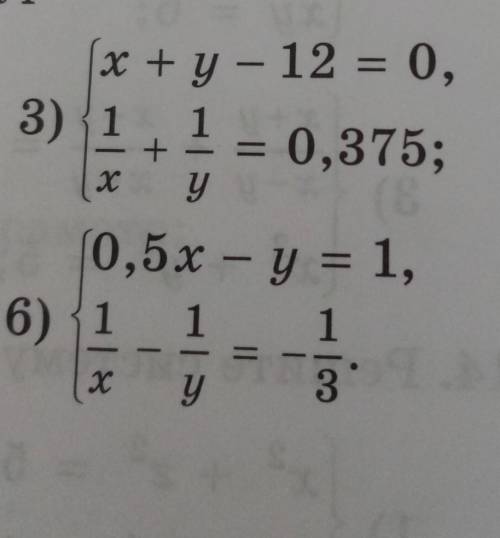
Другие вопросы по теме Алгебра
Популярные вопросы
- Тема что такое отношение? : белых шаров 32 красных 36....
1 - Какое утверждение неверно сила ампера...
1 - Зякою силою треба тягнути дерев яний брусок,масса якого 10кг,по дерев...
2 - Написать сочинение на тему мой родной город петропавловск опорные...
3 - Complete the sentences with prepositions where necessary 1) liz usually...
2 - Знайдіть значення виразу (х-4)+2(4+х)(4-х)+(х+4),якщо х=-1.2...
1 - Нужно составить предложение в past simple и вопросы к нему задать...
3 - Опишите массив из 8 целых чисел, нумерация элементов начинается с...
2 - Приготовить 260 гр раствора соли в котором массовая доля соли составляет...
3 - Хедп в школе мальчики поставляют 57%числа всех учащихся. сколько...
1
Объяснение: