1. Алгебра
  2. решите подстановки систему

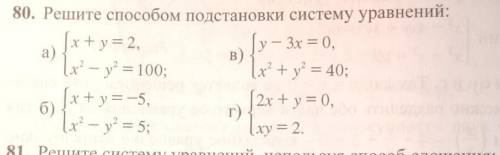
решите подстановки систему уравнений


решите подстановки систему уравнений

MastruevaNasty MastruevaNasty    2   16.09.2021 21:48    0

Ответы
tural23 tural23  16.09.2021 22:00

a)x + y = 2 \\ x {}^{2} - y {}^{2} = 100 \\ x = 2 - y \\ x {}^{2} - y {}^{2} = 100 \\ (2 - y) {}^{2} - y {}^{2} = 100 \\ y = - 24 \\ x = 2 - ( - 24) \\ x = 26 \\

y - 3x = 0 \\ x {}^{2} + y {}^{2} = 40 \\ y = 3x \\ x {}^{2} + y {}^{2} = 40 \\ x {}^{2} + (3x {}^{} ) {}^{2} = 40 \\ x = - 2 \\ x = 2 \\ y = 3 \times ( - 2) \\ y = 3 \times 2 \\ y = - 6 \\ y = 6 \\ - 6 {}^{} - 3 \times ( - 2) = 0 \\ ( - 2) {}^{2} + ( - 6) {}^{2} = 40 \\ 6 - 3 \times 2 = 0 \\ 2 {}^{2} + 6 {}^{2} = 40 \\ 0 = 0 \\ 40 = 40 \\ 0 = 0 \\ 4<img src=

0 = 40 \\ " alt="2x + y = 0 \\ xy = 2 \\ y = - 2x \\ xy = 2 \\ x \times ( - 2x) = 2" />

0 = 40 \\ " />

проверим верно ли равенство :

26 + ( - 24) = 2 \\ 26 {}^{2} - ( - 24) {}^{2} = 100 \\ 2 = 2 \\ 100 = 100

ответ :x=26;y=-24

x + y = - 5 \\ x {}^{2} - y {}^{2} = 5 \\ x = - 5 - y \\ x {}^{2} - y {}^{2} = 5 \\ ( - 5 - y) {}^{2} = 5 \\ y = - 2 \\ x = - 5 - ( - 2) \\ x = - 3

проверим равенство :

- 3 + ( - 2) = - 5 \\ ( - 3) {}^{2} - ( - 2) {}^{2} = 5 \\ - 5 = - 5 \\ 5 = 5 \\

ответ :x=-3;y=-2

Объяснение:

Здесь возможно 2 решения. ответ : x=-2;y=-6

или x=2;y=6

в 4 примере система уравнений не имеет решения

Не забудь обозначить все фигурными скобками. у меня с телефона не получается.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
drshev drshev  23.05.2019 11:11
Изобразите график функцию y=4x-4...
Дима99999910 Дима99999910  23.05.2019 12:00
5cos(2пи+альфа)+4sin(3пи/2 + альфа) найти значение выражения если cos альфа= -1/3...
Piloti3p6i Piloti3p6i  23.05.2019 11:05
Выражение а) (х-2)^2-(х-1)(х+2) б) (5у)^2-2у в) (х-3)(х+3)+2х(2х+3)​...
анна2167 анна2167  23.05.2019 11:04
1. найдите значение выражения 2х3 - у- п у- - 3 2. решите систему уравнений: [5x=2y=11, 3. а) постройте график функции у - 2х - 2. б) определите, проходит ли график функции через...
dasha5334678 dasha5334678  23.05.2019 12:00
Какое из двух чисел меньше: пятизначное или четырехзначное...
mariyaIvanowwwna mariyaIvanowwwna  21.05.2020 11:30
Решите задача ~6 - 7 класса. Сама задача на прикрепленной картинке....
thewitefox thewitefox  21.05.2020 11:37
У выражение икс минус 2 в квадрате минус X - 1 X X + 2 ​...
UskovaV99 UskovaV99  21.05.2020 11:37
Нужно представить дробь в виде произведения...
eva444786 eva444786  21.05.2020 11:37
При якому значенні a рівняння 9x2-12x+a=0 має один корінь? Знайти цей корінь...
Khayalnuriev2005 Khayalnuriev2005  21.05.2020 11:37
1)Разложите на множители: а) 10с * 3 + 15с * 2b б) 5а * 2-20b * 2 2)Постройте в одной системе графики функций y=-4x+3 и y=-5 и найдите координаты точки ихнього сечения. 3) Решите...

Популярные вопросы