РЕШИТЕ ПЕРВЫЕ 2 ЗАДАНИЯ) ЗАРАНЕЕ ">
Другие вопросы по теме Алгебра
Популярные вопросы
- Суммативная работа № 6 за раздел «Сатира и юмор в литературе...
3 - по ангийскому у меня С.О.Р ...
3 - Чого найбільше боялася евеліни сліпий музикант...
1 - Определите тип скелета живых организмов акулы,слизня,божьей коровки...
1 - Сделайте пересказ текста !...
2 - 23-8. Линейная функция 1. Постройте графики функций заданных...
2 - Определи, кем были известные личности, изображенные на портрета....
2 - 3.Определите форму монархи поллюстрации. Eb) сор умоляю 20- ...
2 - 23.3. Өрнектің мәнін табыңдар: 7T4 t33) cos4) tg(-240 );631)...
3 - Was isambard kingdom brunel a political?можно на русском но желательно...
3
Необходимо было решить 2 первые задачи из документа, но я решил ещё и параметр, который мне понравился.
12. Необходимо решить уравнение
Формула двойного угла
А также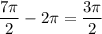 , как известно, добавление или вычитание целого периода из аргумента тригонометрической функции ничего не меняет.
, как известно, добавление или вычитание целого периода из аргумента тригонометрической функции ничего не меняет.
Так как в выражении в скобках присутствует половинный аргумент при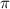 , то косинус поменяется на синус, знак будет отрицательным, потому что если считать, что
, то косинус поменяется на синус, знак будет отрицательным, потому что если считать, что  находится в первой координатной четверти, то при вычислении выражения в скобках значение будет в третьей четверти, где обе функции отрицательны.
находится в первой координатной четверти, то при вычислении выражения в скобках значение будет в третьей четверти, где обе функции отрицательны.
Получаем уравнение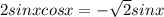 , которое поделим на
, которое поделим на 
Первая часть готова, осталось проанализировать каждую серию решений на принадлежность промежутку![\displaystyle \bigg[-\pi; \frac{3\pi}{2}\bigg]](/tpl/images/1354/0763/31165.png)
Здесь подойдут
Анализируем 2 оставшиеся серии:
Здесь уже необходимо рассматривать отдельно.
Первое с "+" возьмем:
В последней серии решений та же логика, просто исходно дробь будет со знаком "-", значит, в обе части двойного неравенства пойдет с "+"
Теперь можно записывать ответ:
Переходим к 13. Это неравенство.
Сразу видно, что можно заменить на переменную, и тогда неравенство станет куда проще.
можно заменить на переменную, и тогда неравенство станет куда проще.
Если знаменатель больше нуля, то и неравенство будет больше 0. Особый случай - когда числитель равен 1, но , поэтому решением этого неравенство является
, поэтому решением этого неравенство является 
Возвращаемся к замене и решаем относительно :
:
Тогда получается, что и для любого неравенство выполняется.
неравенство выполняется.
ответ: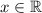
Решение задачи с параметром прикрепляю отдельным документом, так как мне не хватило ограничения на 5000 символов, к сожалению (