Решите очень нужно дякую за відповідь за ответ
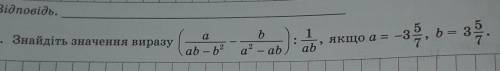
Другие вопросы по теме Алгебра
Популярные вопросы
- Ассоциативный куст»Повесть прочитана, и у каждого из вас сложилось...
1 - Ex 3 p 34. What do you know about the BBC? What else would you like...
1 - Write sentences using the past simple and ago in the correct place.a...
1 - Учебник ваулина 8 класс стр Выписать из текста все формы времени...
1 - Дано розчини солей: Ca(NO3)2, Al(NO3)3, Ba(NO3)2, K2SO4. Виберіть...
3 - Яка кілкість теплоти витрачаеться на те, щоб розплавити 2 кг міді,...
3 - Замініть слова групами залежно від правила написаня букв е,и...
2 - 1. После переключения на другой диапазон частота принимаемой радиоволны...
1 - Хелп ми с естествознанием С 1 страницей:) заранее большое ❤️...
2 - ЧЕТВЕРГ, 26 Ноя 2020 Родной язык (русский)Используя слова съедобный,...
1
1) С начало надо упростить выражение:
Теперь в упрощённое выражение подставляем числа из условия:
В решении.
Объяснение:
Найти значение выражения:
[a/(ab - b²) - b/(a² - ab)] : 1/ab = 0. при а= -3 и 5/7; b= 3 и 5/7.
1) a/(ab - b²) - b/(a² - ab) = (a + b)/ab;
(ab - b²) = b(a - b);
(a² - ab) = a(a - b);
Общий знаменатель: ab(a - b), надписываем над а дополнительный множитель а, над b дополнительный множитель b:
= (a² - b²)/ab(a-b) = (a - b)(a + b)/ab(a - b) = (a + b)/ab;
2) (a + b)/ab : 1/ab =
= (a + b)*ab / ab*1 = a + b =
= - 3 и 5/7 + 3 и 5/7 = 0.