Решите очень надо кр даю 80 б.

Другие вопросы по теме Алгебра
Популярные вопросы
- Определить силу Ампера, действующую на проводникс током длиной 1 метра при силе...
2 - Как вы понимаете слова: «За тыщи вёрст разбросаны могилы тех, кто сажали эти тополя»?...
2 - В чьей душе надежда гибнет,гаснет свет.Руслан и Людмила...
2 - Характеристики героя РОЖДЕСТВО В.В.НАБОКОВ...
1 - Выдели первое неполное делимое запиши сколько цифр должно быть в частном 4662:42...
3 - Как жили рабы в римском обществе какую работу они выполняли?...
1 - Choose the correct item-Steve works at a restaurant, he is ain) Bwaiter Cengineer10...
1 - 1. If she (to be) here we would have seen her.2. I would not agree even if you...
2 - ответьте на во Горы, образовавшиеся на стыке двух литосферных плит 2 Низшая точка...
3 - 2 класс подчеркни в этих предложениях глаголы ...
1
а
б
в
г
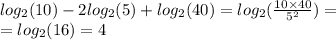
2.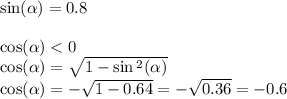
3.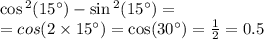
4.а
б
в
г
Проверка:
по знаком корня отрицательные числа, не подходит
ответ: -6
д
Эти же корни в градусах:
ответ: 210°
5.а
знак меняется
Пересекаем с ОДЗ
б
в